题目描述

给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式

第一行包含整数N。

第二行包含N个整数，表示完整序列。

输出格式

输出一个整数，表示最大长度。

数据范围

1≤N≤100000，
−109≤数列中的数≤109

样例

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

二分

由于条件所要求的子序列是单调递增的，且求其最大长度，所以在两个子序列长度相等的情况下，子序列末尾数字越小，越为最优解，而相对数字较大的子序列我们可以直接优化。
即开一数组，下标存储子序列的长度，而其值储存末尾数字，当有数字要插入时，利用二分性质即可找到最优的子序列，（即小于该值的最大值所对应的子序列）

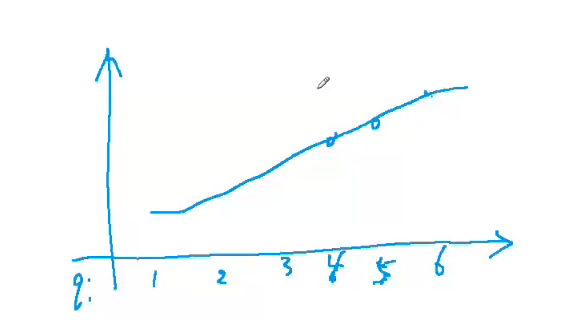
注：存储子序列的长度即末尾值的二维坐标，为单调递增的。见下图y总亲笔图

横坐标为子序列的长度，纵坐标为该子序列最后一位值的大小

C++ 代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 1e6 + 10;
int a[N];
int q[N];
int n;

int main() {
    cin >> n;
    for(int i = 1; i <= n; i ++ ) cin >> a[i];

    int len = 0;
    for(int i = 1; i <= n; i ++ ) {
        int l = 0, r = len;
        while(l < r) {
            int mid = l + r + 1>> 1;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    cout << len << '\n';
    return 0;
}