算法1

(状态机模型) $O(n)$

看到题目以后很直观的感觉是按照数字的位数进行枚举，暴力枚举(例如dfs)也需要总结一个n位数字可能出现的状态，下面开始探索这样的状态有哪些，以及状态之间的相关性。

按照题意，可以出现的数字类型有0、1、2、3且要求的是n位数字的个数，那么对于一个n位数字，可以将其状态定义为：n位中有特定类型数字，且满足0在1前、2在3前的个数。

具体来说：f(n, 0123)表示前n位中同时出现0、1、2、3且满足0在1前、2在3前的数字个数；f(n, 012)表示前n位中同时出现0、1、2且满足0在1前、2在3前的数字个数（当然这里没有3，所有2在3前可以视为妥妥能达到）。

定义了上述状态后，其实可以比较顺畅地想到状态机dp了。在进行状态转移之前，我们可以剔除掉一些无效状态，即肯定不会出现的状态：
f(n, 0) 当n=1时，该状态可以出现，但n>1时，数字不能全是0且n位数大于1，由于本题中满足要求的数字至少4位，所以该状态可以剔除；
f(n, 1) f(n, 3)由于1前面必须出现0，3前面必须出现2，所以不可能单独有1和3出现，该状态可剔除；
……
按照上述类似方法，最终可能出现的状态只能有f(n, 2), f(n, 02), f(n, 01), f(n, 23), f(n, 012), f(n, 023), f(n, 0123)，共6种。

此时需要思考状态之间的转移，按照yxc大佬提高课所授，绘制状态机的转移图如下：

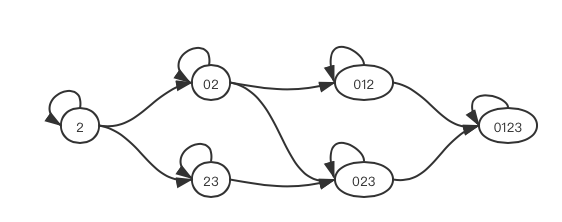
稍微解释下，指向状态0123圈圈的箭头表示，0123状态只能由本身及012和023状态转移过来。

时间复杂度

O(n)

C++ 代码

#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1010, mod = 1e9 + 7;
LL a2, a02, a23, a012, a023, a0123;
LL t2, t02, t23, t012, t023, t0123;
int n;

int main() {
    cin >> n;
    a2 = 1;
    for (int i = 2; i <= n; i++) {
        // 备份
        t2 = a2, t02 = a02, t23 = a23, t012 = a012, t023 = a023, t0123 = a0123;
        a2 = t2 % mod;
        // 系数02表示在末尾可以加上0或2两种，下同
        a02 = (t2 + 2 * t02) % mod;
        a23 = (t2 + t23) % mod;
        a012 = (t02 + 2 * t012) % mod;
        a023 = (t02 + t23 + 2 * t023) % mod;
        a0123 = (t012 + t023 + 2 * t0123) % mod;
    }

    cout << a0123 << endl;

    return 0;
}