题目描述

在图像编码的算法中，需要将一个给定的方形矩阵进行 Z 字形扫描(Zigzag Scan)。

给定一个 n×n 的矩阵，Z 字形扫描的过程如下图所示：

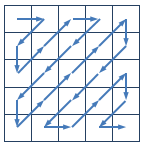
对于下面的 4×4 的矩阵，

1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3
对其进行 Z 字形扫描后得到长度为 16 的序列：1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3。

请实现一个 Z 字形扫描的程序，给定一个 n×n 的矩阵，输出对这个矩阵进行 Z 字形扫描的结果。

样例

输入样例：
4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3
输出样例：
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

算法1

(暴力枚举) $O(n^3)$

根据题解给出的规律，遍历下标和为 0， 1， 2， 3……的点，因为每拐一次弯，以i,j为和的顺序就要互换，所以加了个flag来判断遇到拐点咋走

时间复杂度

参考文献

C++ 代码

#include<iostream>
using namespace std;
const int N = 510;
int f[N][N];
int n;
int main() {
    cin >> n;
    for(int i=0;i<n;i++) {
        for(int j=0;j<n;j++) cin >> f[i][j];
    }
    int flag = 0;
    for(int s = 0; s <= 2*n-2; s ++ ) {
        if(flag) {
            for(int i=0;i<=s;i++) {
                for(int j=s;j>=0;j--) {
                    if(j+i == s && i<n && j<n) cout << f[i][j] << " ";
                }
            } 
        }
        else {
            for(int i=s;i>=0;i--) {
                for(int j=0;j<=s;j++) {
                    if(j+i == s && i<n && j<n) cout << f[i][j] << " ";
                }
            } 
        }  
        flag = !flag;
    }
    return 0;
}