线段树

线段树基于分治思想。啥意思呢？

这里有一段可爱的区间。

表示的是$1-8$。

那么接下来我们对这个区间进行一些操作：

这个不难办，直接改就行了。

但接下来这个呢？

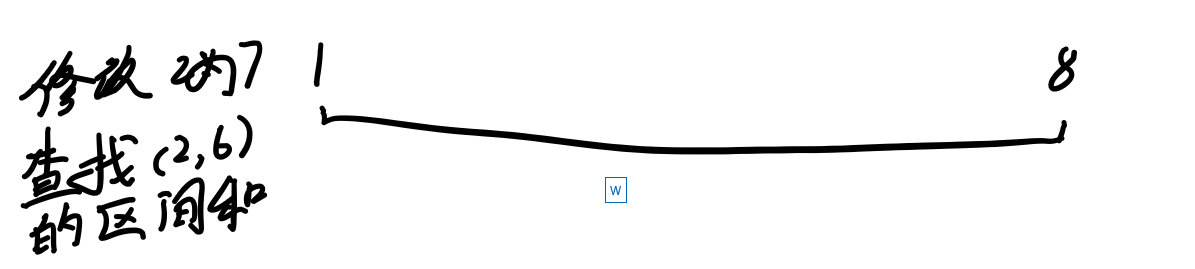
考虑修改运算，如果直接建数组的话可以$O(1)$维护，直接a[x] = v就行了。

但是查询运算就是费劲了。

这样的话我们需要遍历，o(N)有点毒瘤。

我们还可以用前缀和优化，但好像也每快多少。

接下来先别慌，虽然后面有点高能，先回忆一下这个。

然后我们突然想到分治思想。

分治的话在很多算法中都有用到，是非常常用而且非常简单的一种算法。

可以从字面上来理解，就是“分而治之”的意思。

那么我们可以把每一个区间一分为二，这样就把整个区间变成了一棵树。

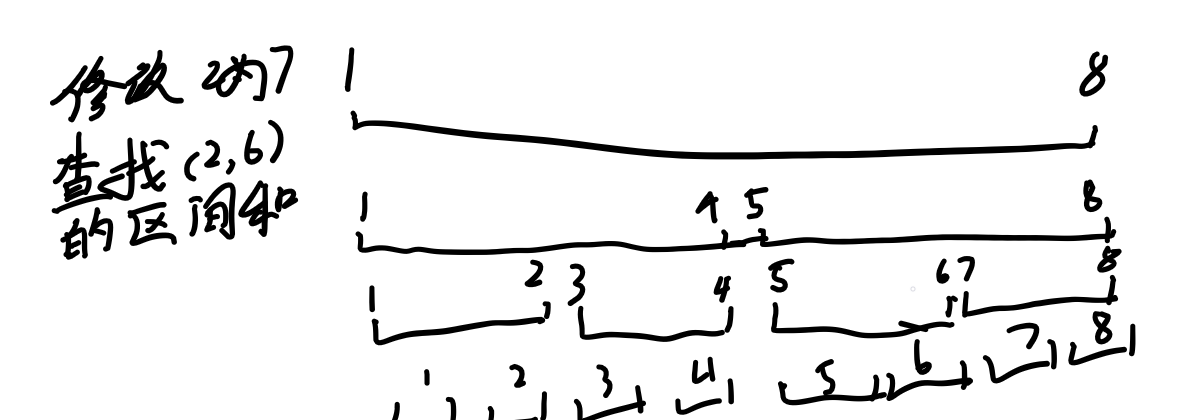
这样的话我们可以看一下两个操作，因为是树上，而且是一棵满二叉树，所以深度一定是$O(log N)$的。

这样两个操作都是logn了，秀到飞起。

所以说这样就好了呀~

我们来看一些基本的操作吧！

首先是上传的操作，线段树的意思就是用左右子树更新根节点。

这个操作有名字，叫pushup。

怎么写呢？

这个的话我们结合着拿到题写吧。

就是单点修改，区间查询。

线段树的话一般使用结构体维护。

结构体里想要啥有啥放进去就行了。

struct Node
{
    int l, r;//左右端点区域

    int sum;//各种查询变量存储区域

    //最后还有个懒标记区域，一般在区间修改时使用。
}tr[N * 4];//4倍空间

那么的话pushup的操作就是用左右两边的区间更新总区间。

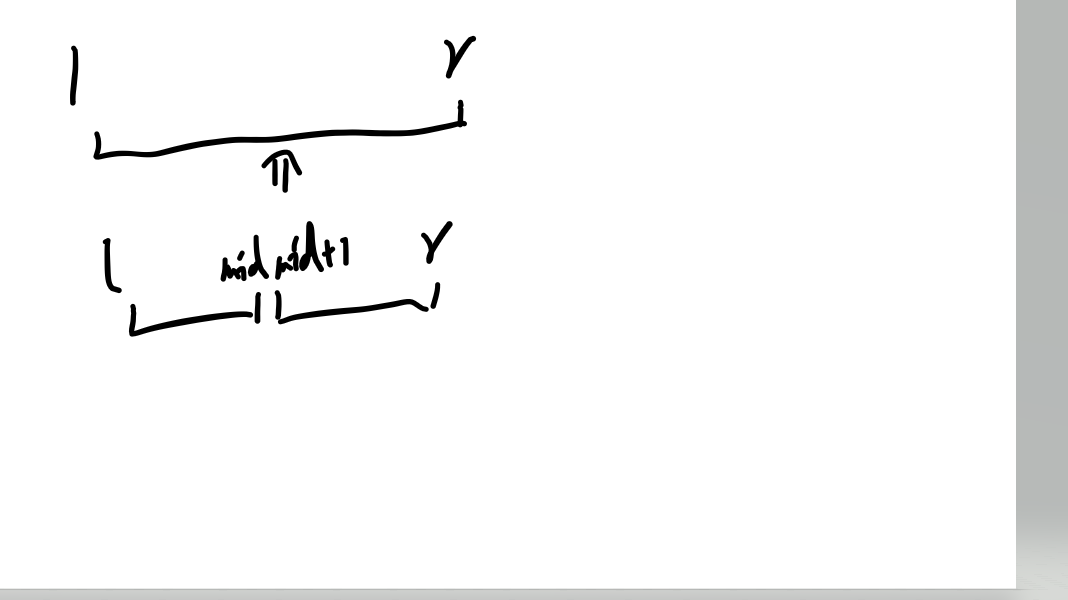
这个的话很简单，大区间等于小区间的和。

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

然后就是建树操作，在最开始需要把树“建造出来”。

这个可以直接递归建立树。

这个的话可以分治处理。

先用一张图分析一下吧。

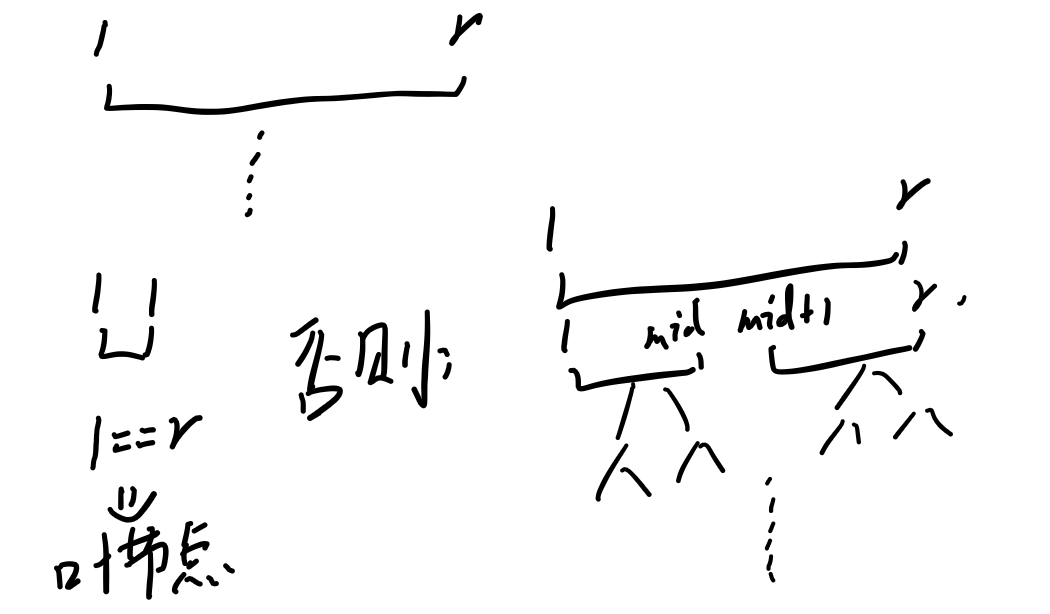
那么的话我们试着捋一下逻辑。

首先的话是判断一下是否是叶节点。

否则的话就分段处理就行。

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

然后就是变化操作和查询操作。

变化操作就是直接搜就行了。

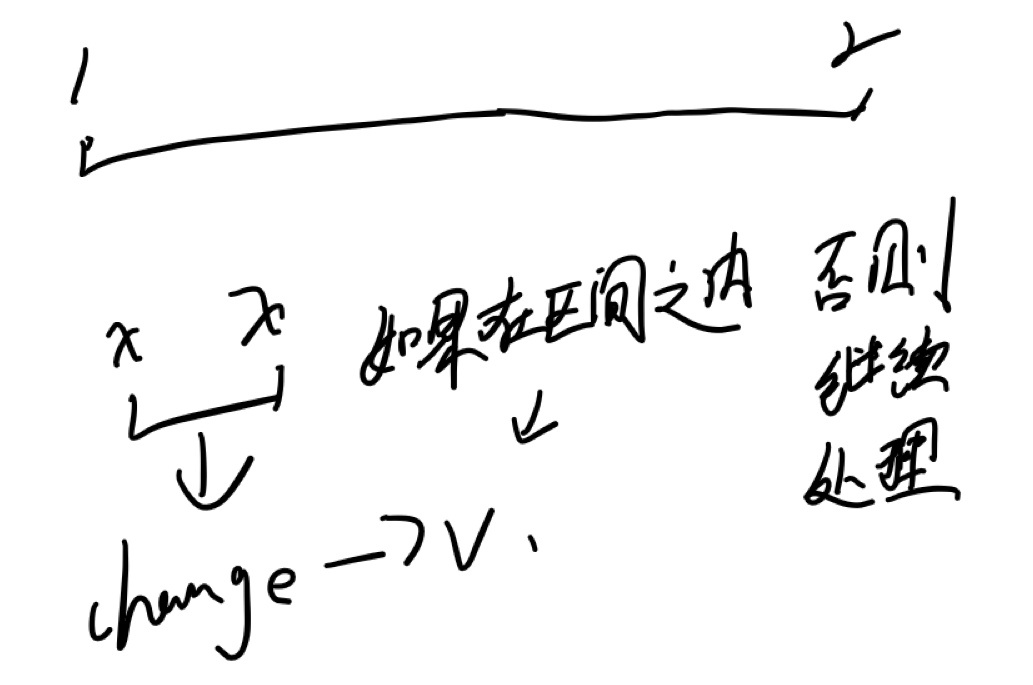
这个跟build很类似，没有什么太大的难度，而且是单点修改，很水哦。

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

然后是查询操作。

这个也不难。

就可以直接判断区间。

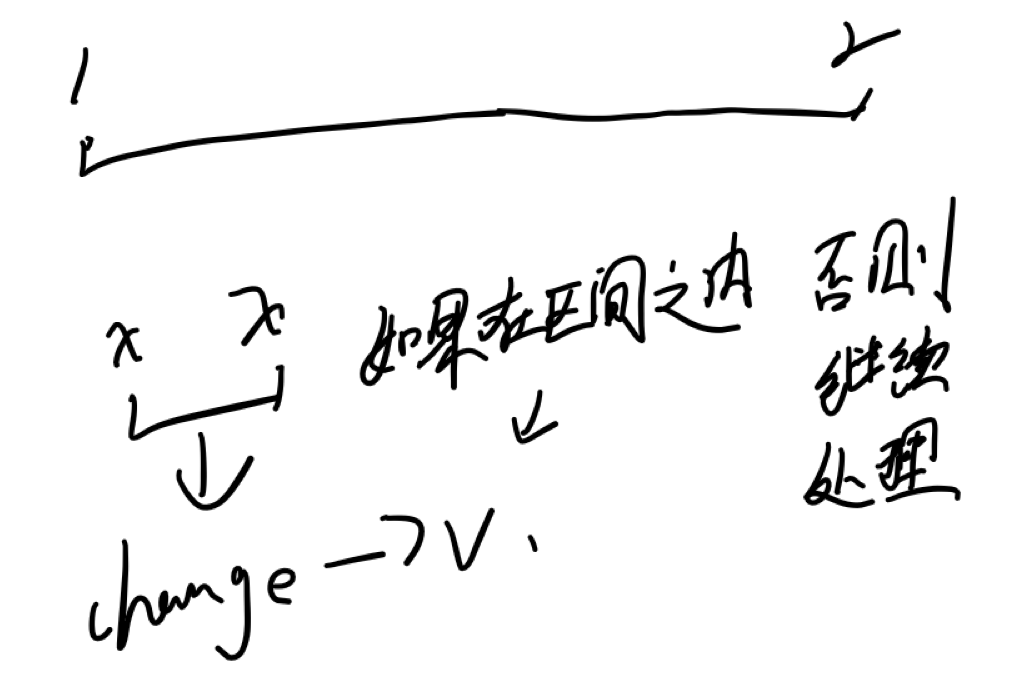
那么的话我们来康一下代码吧：

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if(l <= mid) v = query(u << 1, l, r);
    if(r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

线段树的思想上面已经说完了，那么就是代码了：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
int w[N];
struct Node
{
    int l, r;
    int sum;
}tr[N * 4];
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void build(int u, int l, int r)
{
    if(l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}
void change(int u, int x, int v)
{
    if(tr[u].l == x && tr[u].r == x) 
    {
        tr[u] = {x, x, tr[u].sum + v};
    }
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) change(u << 1, x, v);
        else change(u << 1 | 1, x, v);
        pushup(u);
    }
}
int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(r <= mid) return query(u << 1, l, r);
        else if(l > mid) return query(u << 1 | 1, l, r);
        else
        {
            int left = query(u << 1, l, r);
            int right = query(u << 1 | 1, l, r);
            int ans;
            ans = left + right;
            return ans;
        }

    }
} 
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        cin >> w[i];
    }
    build(1, 1, n);
    while(m --)
    {
        int op, l, r;
        cin >> op >> l >> r;
        if(op == 0)
        {
            cout << query(1, l, r) << endl;
        }
        else
        {
            change(1, l, r);
        }
    }
    return 0;
}