题目描述

求把$N * M$的棋盘分割成若干个$1*2$的的长方形，有多少种方案。

例如当N=2，M=4时，共有5种方案。当N=2，M=3时，共有3种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数N和M。

当输入用例N=0，M=0时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

$1 \leq N, M \leq 11$

样例

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

状态压缩dp

状态表示f[i][j]

集合：第i列，j为上一列伸过来的头的不同方案（二进制表示）。

属性：方案总数

状态计算：

对符合的条件相加 f[i][j] += f[i - 1][k]

对于放满这种问题，我们只需找出所有可以横着放的木块的方案，即为全部方案。
我们用j的二进制表示来代替第i列的不同情况（横着放的木块中，该列由上一列伸过来的头的情况）

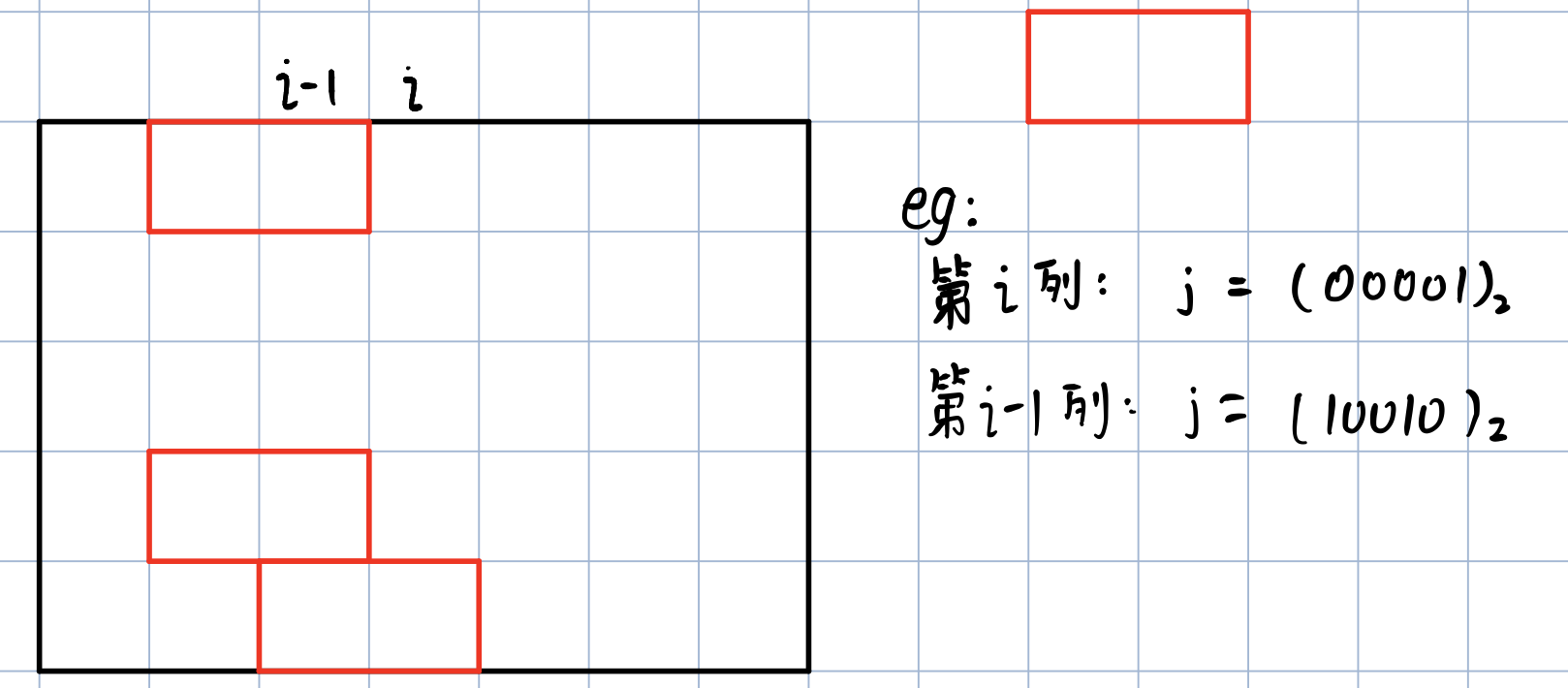
若最后要合法放置且放满：

每次可看做为判读第i - 1列
条件一：第i - 1列伸出去的头与第i - 2列伸过来的头不可重复
条件二：第i - 1列相邻放置横木块的中间必须为2的倍数，否则一定会空出格子

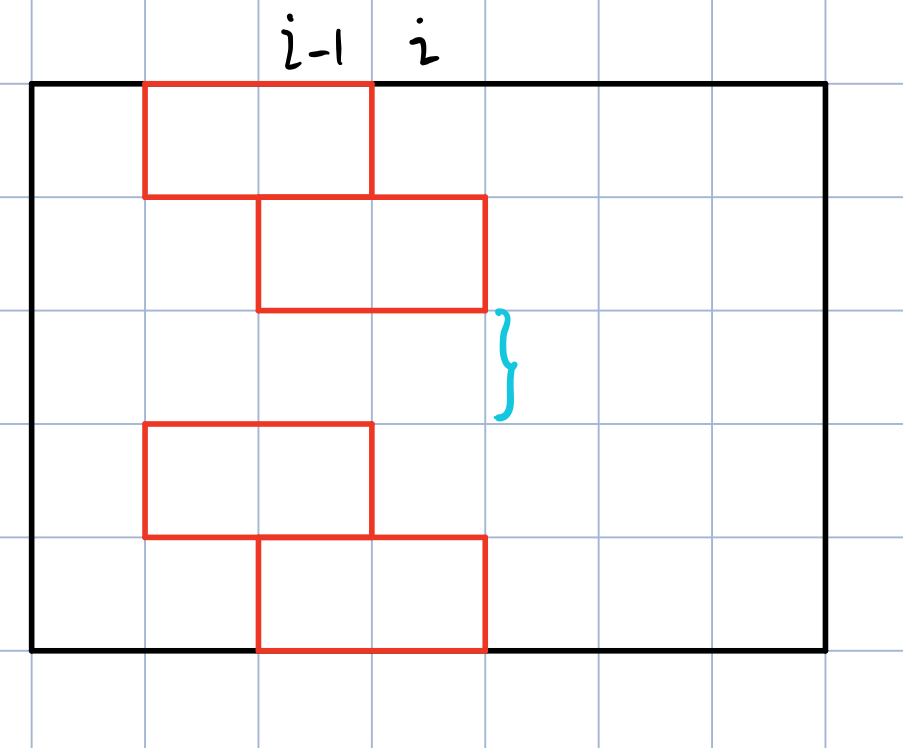
如图，蓝色圈出的行数为1，放不下竖立的木块，故该种方法是不合法的。

C++ 代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 15, M = 1 << N;
long long f[N][M];
bool st[M];//判断是否可以放满

int main() {
    int n, m;
    while(cin >> n >> m, n || m) {
        memset(f, 0, sizeof(f));

        int cnt = 0;//表示两横放物块的间距
        //预处理出合法不合法的情况
        for(int i = 0; i < 1 << n; i ++ ) {
            cnt = 0;
            st[i] = true;
            for(int j = 0; j < n; j ++ ) {
                if((i >> j) & 1 ) {//当前行木块横着放
                    if(cnt & 1) {
                        //间距为奇数，不成立
                        st[i] = false;
                        break;
                    }
                    cnt = 0;
                }
                else cnt ++ ;
            }
            if(cnt & 1) st[i] = false;//判断最后剩下的一块的间距
        }

        f[0][0] = 1;//表示一种方案（第1列没有上一列神过来的头）
        for(int i = 1; i <= m; i ++ ) //要处理到比棋盘多一列的位置
            for(int j = 0; j < 1 << n; j ++ ) 
                for(int k = 0; k < 1 << n; k ++ ) {
                    if((j & k) == 0 && st[j | k] == true) 
                        f[i][j] += f[i - 1][k];
                }

        cout << f[m][0] << '\n';//棋盘外第一列没有伸出来头的数量

    }

    return 0;
}