算法

(图论,基环树,找环) $O(n)$

由题意，我们需要在所有点的出度均是1的有向图中，求出最小环的长度。

在有向图中找环有很多算法，比如求有向图强联通分量的Tarjan算法等，但杀鸡焉用宰牛刀，这个图很特殊，我们可以使用迭代的方式来做。

注意当题目中点数很大时，如果能用迭代的方式，就尽量不要使用递归的方式，因为可能存在爆栈的问题。

首先我们考虑一下所有点的出度均是1的有向图的性质，其中的每个连通块的形状都是这样的：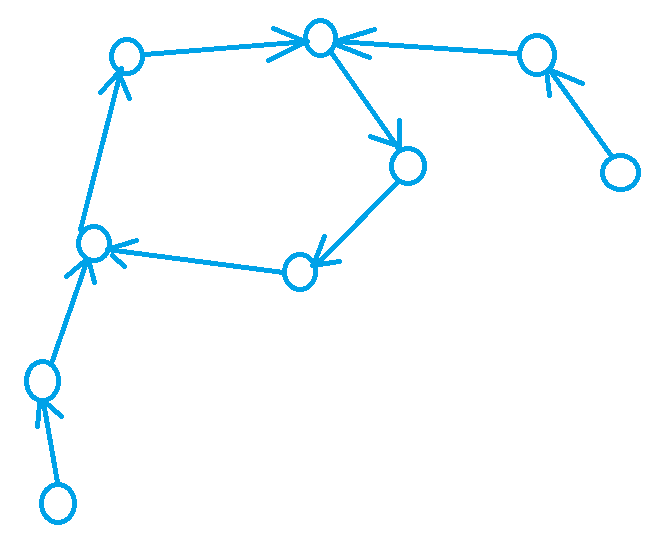

即一个环上挂着很多树，而且不管从哪个点出发，最终都会走到某个环上。

因此我们可以借助于栈结构来找出所有环：

• 从前往后扫描每个点，如果当前点没有被遍历过，则沿着出边一直走，直到走到已经被遍历过的点为止，走的过程中将所有点按顺序存入栈中。此时会有两种情况：

  • 此时走到的已被遍历过的点在栈中，则栈中从该点开始，到当前点这部分就是环上的所有点；
  • 此时走到的已被遍历过的点不在栈中，则说明当前只是在某个分支上走，并没有走到某个环上；

所有环的长度的最小值即是答案。

时间复杂度

每个点只会进栈依次，出栈依次，因此总时间复杂度是 $O(n)$。

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 200010;

int n;
int p[N], stk[N];
bool st[N], in_stk[N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &p[i]);

    int res = n;
    for (int i = 1; i <= n; i ++ )
        if (!st[i])
        {
            int tt = 0;
            int j = i;
            while (!st[j])
            {
                stk[ ++ tt] = j;
                st[j] = true;
                in_stk[j] = true;
                j = p[j];
            }
            if (in_stk[j])
            {
                int cnt = 1;
                while (stk[tt] != j)
                {
                    in_stk[stk[tt -- ]] = false;
                    cnt ++ ;
                }
                res = min(res, cnt);
            }
            while (tt) in_stk[stk[tt -- ]] = false;
        }

    printf("%d\n", res);
    return 0;
}