题目链接： 地宫取宝

动态规划：
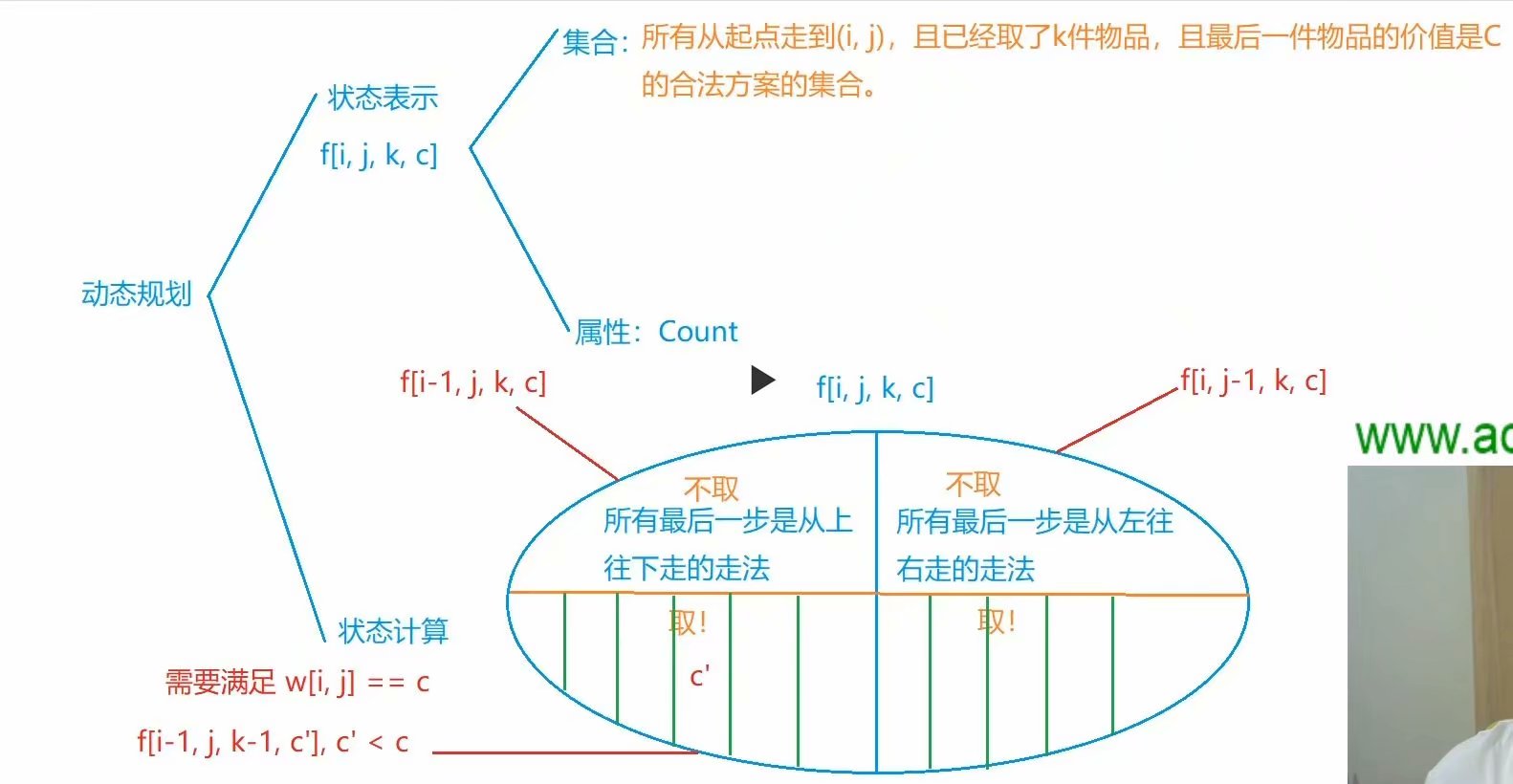
状态表示：
f[i][j][k][c]
集合：所有从起点走到(i,j)上，已经取了k个物品，并且取得的物品最大价值是c，也就是最后一件物品的价值是c的集合。
属性：数量
状态计算：
分为四维，首先是从左边过来的或者是从上边过来的，然后就是取了(i,j)上的物品还是没有取
难点就是在于状态计算的部分，想想01背包问题，不选(i,j)的话，就直接把上一个状态转移过来，选的话就要考虑背包是都放得下的问题。

这个题不选的话：直接把上一步k,c的状态转移过来，
如果选的话，必须满足c==w[i][j]时，选了w[i][j]就说明w[i][j]是所选物品价值的最大值，那上一步就应该选了k−1个物品，而且上一步身上所有物品最大值只能是1…c−1，把这些状态的方案数累加，就可以成为选择当前物品的条件。
注：

因为这道题的所有物品价值范围是0…12，可以把他们全部都递增，范围就变成了1…13，因为我们记录的是方案数，只关心各个物品之间的大小关系，具体数值不影响答案，但是这样的做法可以把0作为一个特殊边界来处理
整个过程不理解的话，可以用纸笔模拟一下，看看每个状态的数值应该是多少

#include <iostream>
#include <cstring>
using namespace std; 
const int MOD=1000000007 ,N=55;
int f[N][N][13][14];
int w[N][N];
int n,m,k;
int main(int argc, char** argv) {
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&w[i][j]);
            w[i][j]++;
        }
    }
    //两个边界初始化
    //在起点(1, 1)处
    //如果拿也只能拿a [i][j]这个物品，只有一种方案
    //如果不拿，那就是0个物品，也是一个方案数
    //由于物品价值已经增加了一个偏移量，现在价值的范围是[1, 13]
    //所以价值为0并不代表物品的价值，而是一个边界点
    f[1][1][1][w[1][1]]=1;
    f[1][1][0][0]=1;//f[1][1][0][-1] //-1就是一个物品也不选，比价值是0还要小的价值，由于数组下标没有负的，所以价值整体加1
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i==1&&j==1)  continue;
            for(int u=0;u<=k;u++){
                for(int v=0;v<=13;v++){
                    //不取(i,j)
                    int &val=f[i][j][u][v];//由于下面要多次用到f[i][j][u][v],所以最好用一个简单的变量代替
                //这句话的意思是 f[i][j][u][v]的值跟着val的值的改变
                    val=(val+f[i-1][j][u][v])%MOD;
                    val=(val+f[i][j-1][u][v])%MOD;
                    //取(i,j)
                    if(v==w[i][j]){
                        for(int c=0;c<v;c++){
                            val=(val+f[i-1][j][u-1][c])%MOD;
                            val=(val+f[i][j-1][u-1][c])%MOD;
                        }
                    }
                }
            }
        }
    }
    int res=0;
    for(int i=1;i<=13;i++){
        res=(res+f[n][m][k][i])%MOD;
    }
    cout<<res;
    return 0;
}