题目描述

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [u_i, v_i]，表示 u_i 和 v_i 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

返回所有连通三元组中度数的 最小值，如果图中没有连通三元组，那么返回 -1。

样例

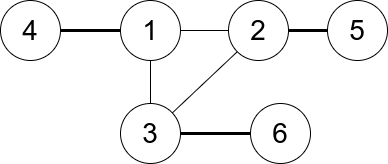
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

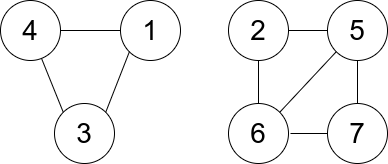
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0。
2) [2,5,6]，度数为 2。
3) [5,6,7]，度数为 2。

限制

• 2 <= n <= 400
• edges[i].length == 2
• 1 <= edges.length <= n * (n-1) / 2
• 1 <= u_i, v_i <= n
• u_i != v_i
• 图中没有重复的边。

算法

(暴力枚举) $O(n^3)$

1. 枚举所有的连通三元组，求其度数。
2. 连通三元组的度数为三个顶点的度数之和减 6。
3. 可以通过点的序号关系，降低枚举中时间复杂度的常数，避免重复的枚举。

时间复杂度

• 连通三元组的个数就已经是 $O(n^3)$ 的，所以总时间复杂度为 $O(n^3)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储图的邻接表和邻接矩阵，以及每个点的度数。

C++ 代码

class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        vector<vector<bool>> map(n + 1, vector<bool>(n + 1, false));
        vector<vector<int>> graph(n + 1);
        vector<int> deg(n + 1, 0);
        for (const auto &e : edges) {
            map[e[0]][e[1]] = map[e[1]][e[0]] = true;
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
            deg[e[0]]++;
            deg[e[1]]++;
        }

        int ans = INT_MAX;
        for (int i = 1; i <= n; i++) {
            sort(graph[i].begin(), graph[i].end());
            for (int j = 0; j < graph[i].size(); j++) {
                if (graph[i][j] < i) continue;
                for (int k = j + 1; k < graph[i].size(); k++) {
                    int v0 = graph[i][j], v1 = graph[i][k];
                    if (map[v0][v1] && ans > deg[i] + deg[v0] + deg[v1] - 6)
                        ans = deg[i] + deg[v0] + deg[v1] - 6;
                }
            }
        }
        if (ans == INT_MAX)
            ans = -1;
        return ans;
    }
};