题目描述

Ural大学有N名职员，编号为1~N。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 Hi 给出，其中 1≤i≤N。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式

第一行一个整数N。

接下来N行，第 i 行表示 i 号职员的快乐指数Hi。

接下来N-1行，每行输入一对整数L, K,表示K是L的直接上司。

输出格式

输出最大的快乐指数。

数据范围

$1 \leq N \leq 6000$
$-128 \leq H_i \leq 127$

样例

输入样例：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

输出样例：

5

树形dp

状态表示f[u][0],f[u][1]:

集合：f[u][0]表示从u结点的子树中寻找点，但不包括u点的集合，f[u][1]表示包含u结点

属性：最大值Max

状态计算

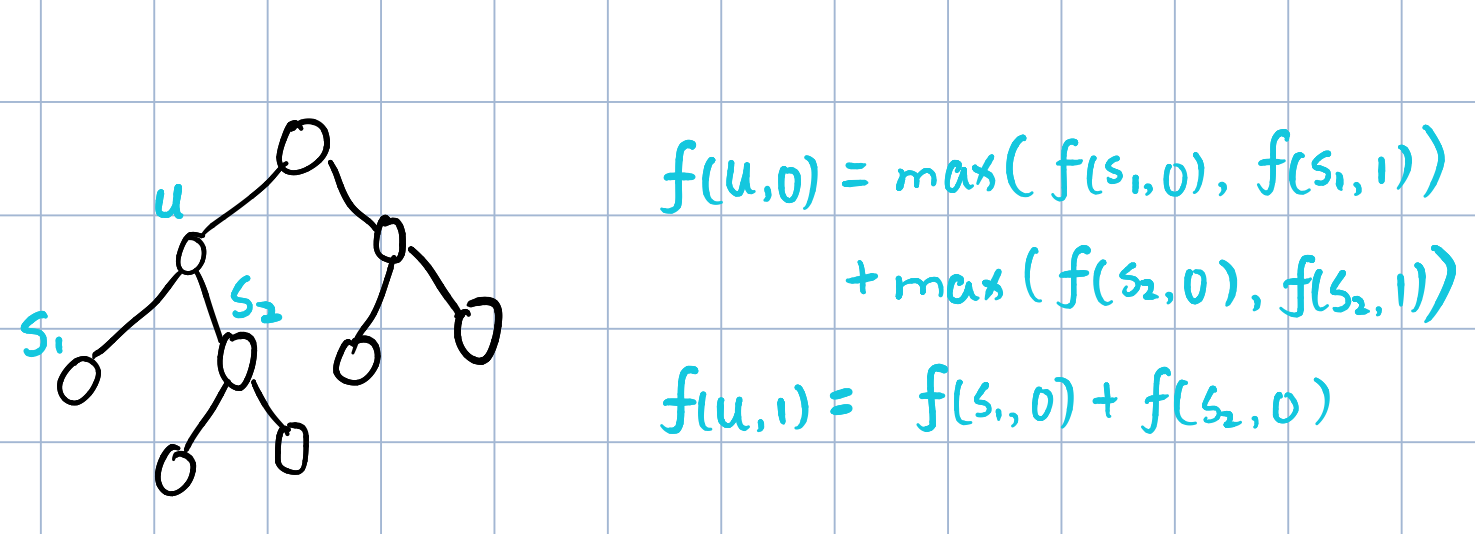
C++ 代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 6010;
int happy[N];
int h[N], e[N], ne[N], idx;
bool st[N];
int f[N][2];
int n;

void add(int a, int b);
void dfs(int u);

int main() {
    memset(h, -1, sizeof(h));
    cin >> n;
    for(int i = 1; i <= n; i ++ ) cin >> happy[i];
    for(int i = 0; i < n - 1; i ++ ) {
        int a, b;
        cin >> a >> b;
        st[a] = true;
        add(b, a);
    }

    int root = 1;//寻找根节点
    while(st[root]) root ++ ;

    dfs(root);

    cout << max(f[root][0], f[root][1]) << '\n';

    return 0;
}
void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++ ;
}
void dfs(int u)
{
    f[u][1] = happy[u];

    for(int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        dfs(j);
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}