题目描述

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式
共q行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：
17
27
21

算法

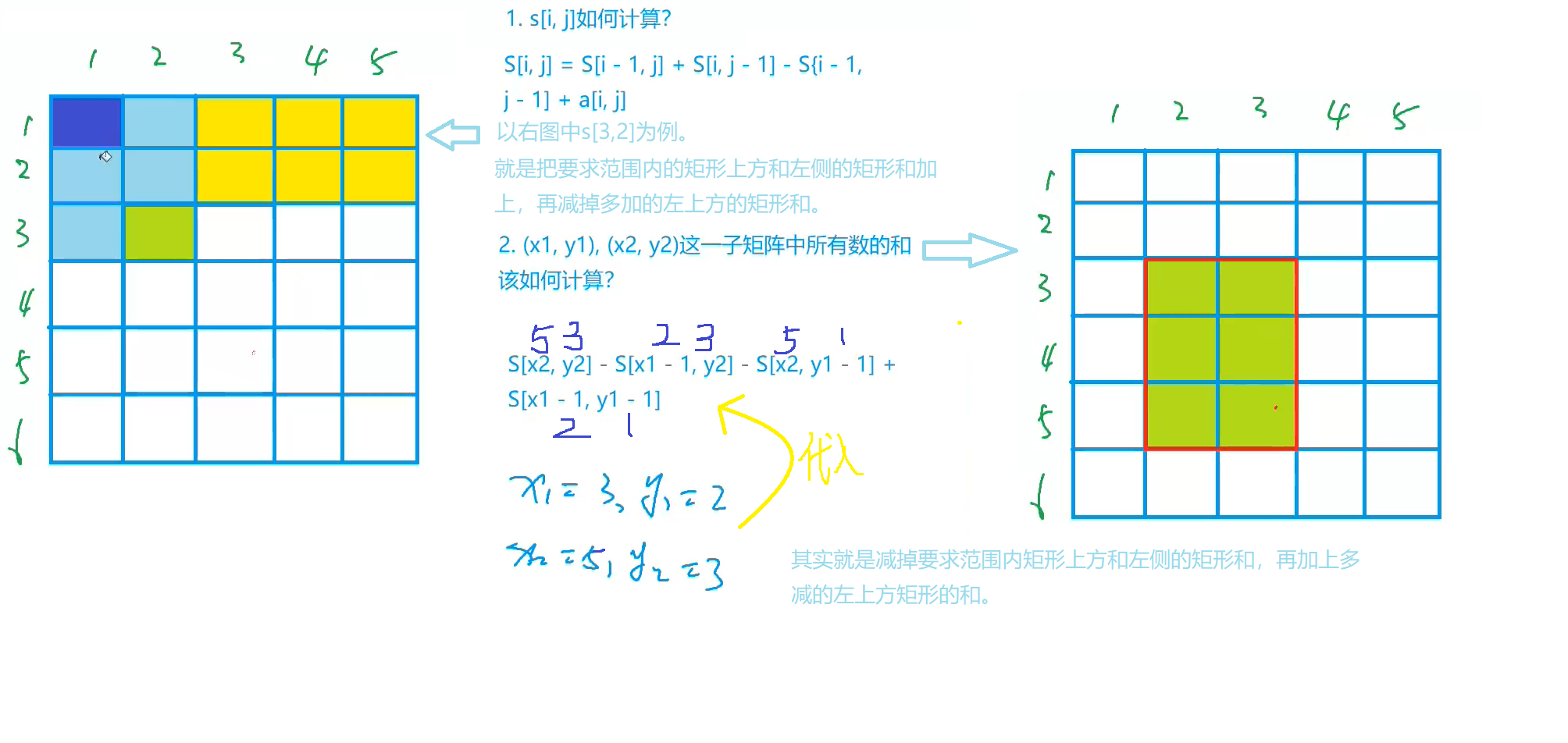
推导公式？

参考文献

y总讲解视频

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int n , m,q;
//a数组保存原矩阵的值  s数组保存从s[1,1]到s[i][j]中这个矩阵内所有数的和
int a[N][N] ,s[N][N];

int main(){
    cin>>n>>m>>q;
    //下标从1开始，避免一些边界的问题
    for(int i = 1; i <= n ; i++){
        for(int j = 1; j <= m ;j++){
            cin>>a[i][j];
        }
    }
    //也是从1下标开始，求出每个位置保存的值
    for(int i = 1; i <= n ; i++){
        for(int j = 1; j <= m ;j++){
            //s[i][j]等于上方矩形和左方矩形以及本身所占位置的a[i][j]
            //这三个位置的总和，再减掉多加上的左上方矩形。
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    while(q--){
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        //（x1,y1)和(x2,y2)围成的矩形和也是同理，即减掉上方矩形和左侧矩形
        //以及加上多减的左上方矩形的总和，就是要求的答案。
        printf("%d\n",s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}