题目描述

给定一个句法二叉树，请你输出相应的中缀表达式，并利用括号反映运算符的优先级。

输入格式

第一行包含整数 N 表示二叉树的总结点个数。

接下来 N 行，每行以下列格式给出一个结点的信息（第 i 行对应于第 i 个结点）：

data left_child right_child

其中 data 是一个长度不超过 10 的字符串，left_child 和 right_child 分别是该结点的左右子结点编号。

所有结点编号从 1 到 N，NULL 用 -1 表示。

输出格式

请在一行输出中缀表达式，并利用括号反映运算符的优先级。
注意，不能有多余括号，请任何符号之间不得有空格。

数据范围

1≤N≤20

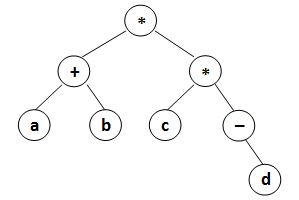
输入样例1

8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1

输出样例1：

(a+b)*(c*(-d))

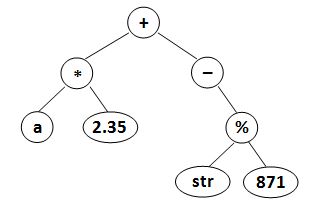
输入样例2：

8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1

输出样例2：

(a*2.35)+(-(str%871))

思路

1、数据处理加找到根节点

2、只要想明白一个问题：二元运算必须有符号右边那个式子，即根据数据构建完树后的右孩子

故在递归遍历树的时候，只要判断该节点是否有有孩子

然后返回的字符串数: 递归左子树的string值 + 该节点的string值 + 递归右子树的string值

3、如果该节点不是根节点 则在该返回值的左右两边加上括号

4、最后输出返回值

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 30;

int n;
string w[N];
int l[N], r[N], indegree[N];
bool isleaf[N];

string dfs(int u)
{
    string left,right;
    if(l[u] != -1)
    {
        left = dfs(l[u]);
        if(!isleaf[l[u]]) left = "(" + left + ")";
    }
    if(r[u] != -1)
    {
        right = dfs(r[u]);
        if(!isleaf[r[u]]) right = "(" + right + ")";
    }
    return left + w[u] + right; 
}

int main()
{
    cin >> n;
    int root;

    for(int i = 1; i <= n; i ++ )
    {
        cin >> w[i] >> l[i] >> r[i];
        if(l[i] != -1) indegree[l[i]] ++;
        if(r[i] != -1) indegree[r[i]] ++;
        if(l[i] == -1 && r[i] == -1) isleaf[i] = true;
    }
    for(root = 1; root <= n; root ++ ) if(!indegree[root]) break;
    cout << dfs(root);
    return 0;
}