题目描述

原题

输入一个长度为n的整数序列。

接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。

第二行包含n个整数，表示整数序列。

接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式
共一行，包含n个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：
3 4 5 3 4 2

算法

推导公式，详见代码注释，以及下方的图解推导。

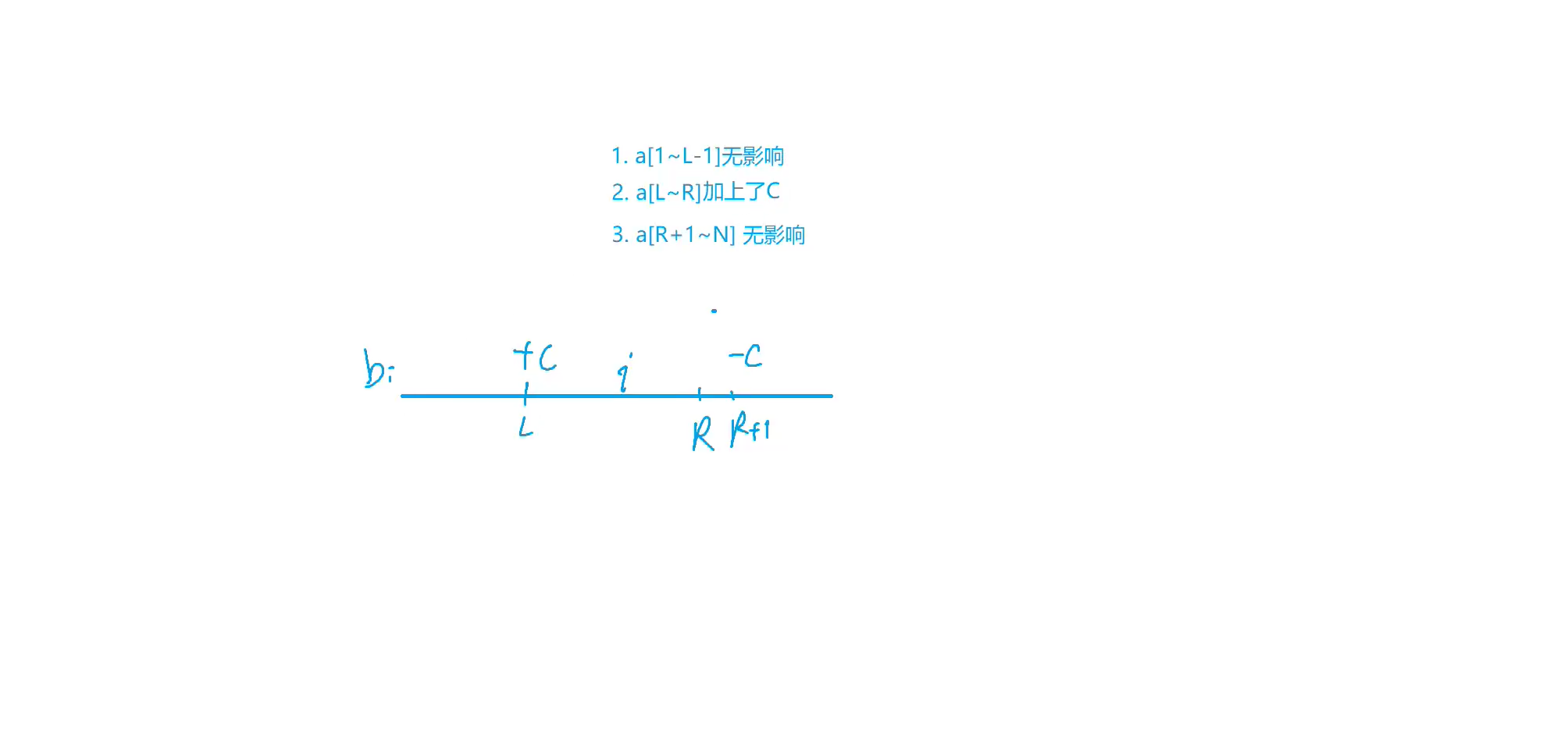
比如给定一个a[n]的数组，构造差分数组b [N] ,使得a [i] = b[1] + b[2] + b[3] + ….+ b[i]。（a[i] 是b数组的前缀和）

差分的核心操作：

将a[L,R] 之间的数加上C，就等价于 b[L] += C ,b[R + 1] -= C。

我们知道差分和前缀和是逆运算，a是原数组，b是差分数组，他们之间的关系满足：
a[i] = b[0] + b[1] +…+ b[i];
a[i]的值就是b[i]的前缀和，所以我们在a数组（L，R）之间加上c的时候就是等价于
在b数组的b[L]点处加上c！这里特别注意虽然只是在b[L]这一点上加上C，但是我们在
求a数组的时候就是求b数组的前缀和，所以在求的时候就会在（L，R）这个区间每一次
都加了一次c，这也就相当于在L—R这个区间加了c。而b[r + 1] -=c,就是为了防止
在区间的后买了多加了c值，前面的话是不影响的。

原因看下图解：

参考文献

y总讲解视频

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;
int n,m;
//a：题目给定的数组   b：差分数组
int a[N],b[N];

/*
我们知道差分和前缀和是逆运算，a是原数组，b是差分数组，他们之间的关系满足：
a[i] = b[0] + b[1] +...+ b[i];
a[i]的值就是b[i]的前缀和，所以我们在a数组（L，R）之间加上c的时候就是等价于
在b数组的b[L]点处加上c！这里特别注意虽然只是在b[L]这一点上加上C，但是我们在
求a数组的时候就是求b数组的前缀和，所以在求的时候就会在（L，R）这个区间每一次
都加了一次c，这也就相当于在L---R这个区间加了c。而b[r + 1] -=c,就是为了防止
在区间的后买了多加了c值，前面的话是不影响的。
*/
void insert(int l ,int r , int c){
    b[l] += c;
    b[r + 1] -= c;
}

int main(){
    cin>>n>>m;
    for(int i = 1 ; i <= n; i++){
        cin>>a[i];
        //进行n步插入操作,构造差分数组
        insert(i,i,a[i]);

    }

    //m次操作
    while(m--){
        int l , r , c;
        cin>>l>>r>>c;
        //一次操作的插入，对差分数组b进行改变
        insert(l,r,c);
    }

    //求改变之后的数组a
    for(int i = 1 ;i <= n ;i++){
 //求m次操作之后的数组，这里是一个推导公式a[i] = b[0] + b[1] +...+ +b[i]的变形
//公式推导在下方
        a[i] = a[i - 1] + b[i];
        cout<<a[i]<<' ';
    }
    return 0;

}

a[i] = a[i - 1] + b[i]的推导：

a[o] = b[0]的， b[1] = a[1] - a[0]是a[1]的变形带入到a[2]里面去，最终就会发现
a[i] = a[i - 1] + b[i];