题目描述

给定二叉树根结点 root，此外树的每个结点的值要么是 0，要么是 1。

返回移除了所有不包含 1 的子树的原二叉树。

（回想结点 X 的子树为 X 本身，以及所有 X 的后代。）

样例

输入：[1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色结点满足条件“所有不包含 1 的子树”。
右图为返回的答案。

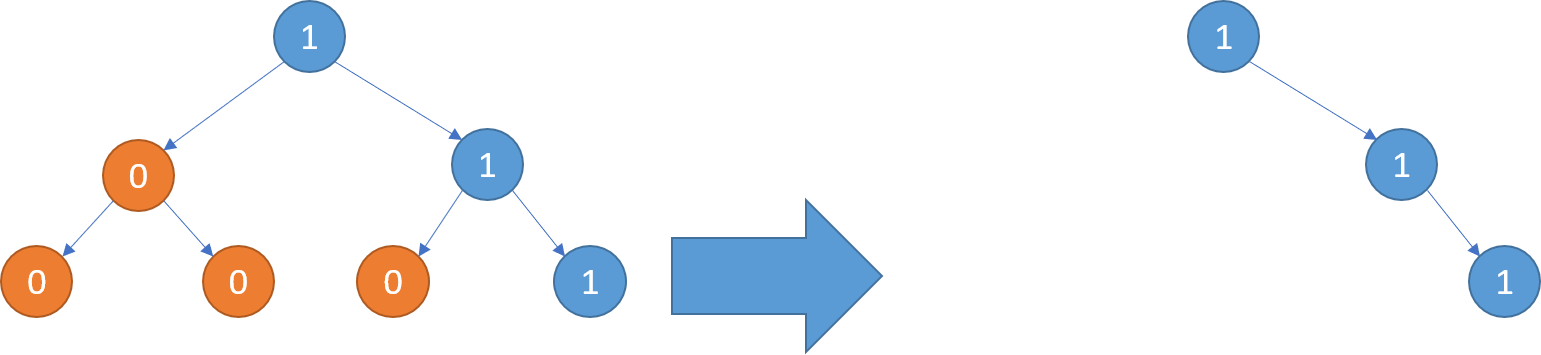
输入：[1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

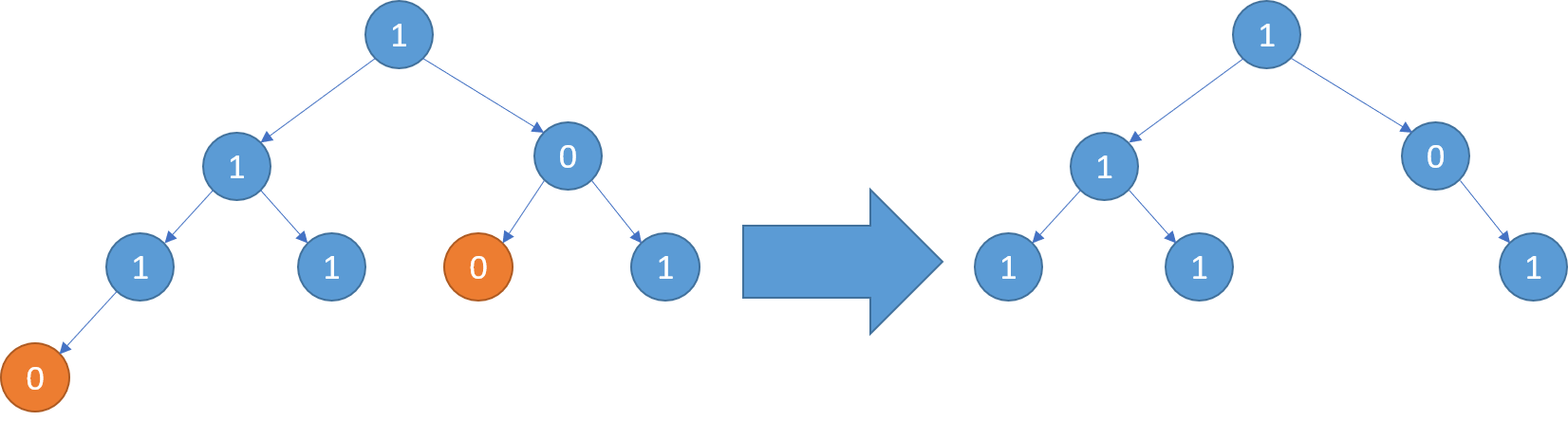
输入：[1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]

提示

• 给定的二叉树最多有 100 个结点。
• 每个结点的值只会为 0 或 1。

算法

(递归) $O(n)$

1. 很容易想到可以通过递归来解决这个问题。
2. 设函数 solve(TreeNode *rt) 返回以 rt 为根的子树是否包含 1。
3. 在函数体中，如果 rt 为空则直接返回 false。然后递归左子树，如果递归结果返回的是 false，则左子树置为空；右子树同理。
4. 如果左右子树均为空，且 rt 的值也是 0，则返回 false；否则返回 true。

时间复杂度

• 每个结点遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 递归需要占用系统栈空间，故空间复杂度为 $O(h)$，其中 $h$ 为树的高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool solve(TreeNode *rt) {
        if (rt == NULL)
            return false;
        if (!solve(rt -> left))
            rt -> left = NULL;
        if (!solve(rt -> right))
            rt -> right = NULL;

        if (rt -> left == NULL && rt -> right == NULL)
            return rt -> val == 1;

        return true;
    }

    TreeNode* pruneTree(TreeNode* root) {
        if (!solve(root))
            return NULL;
        return root;
    }
};