动态规划

要点：
1.本题是摘花生和最长上升子序列的结合，没做过的可以先做下前两道，思路会更清晰些
2.（如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它）说明拿的价值是递增的

        Scanner scanner=new Scanner(System.in);
        int n=scanner.nextInt(),m=scanner.nextInt(),k=scanner.nextInt();
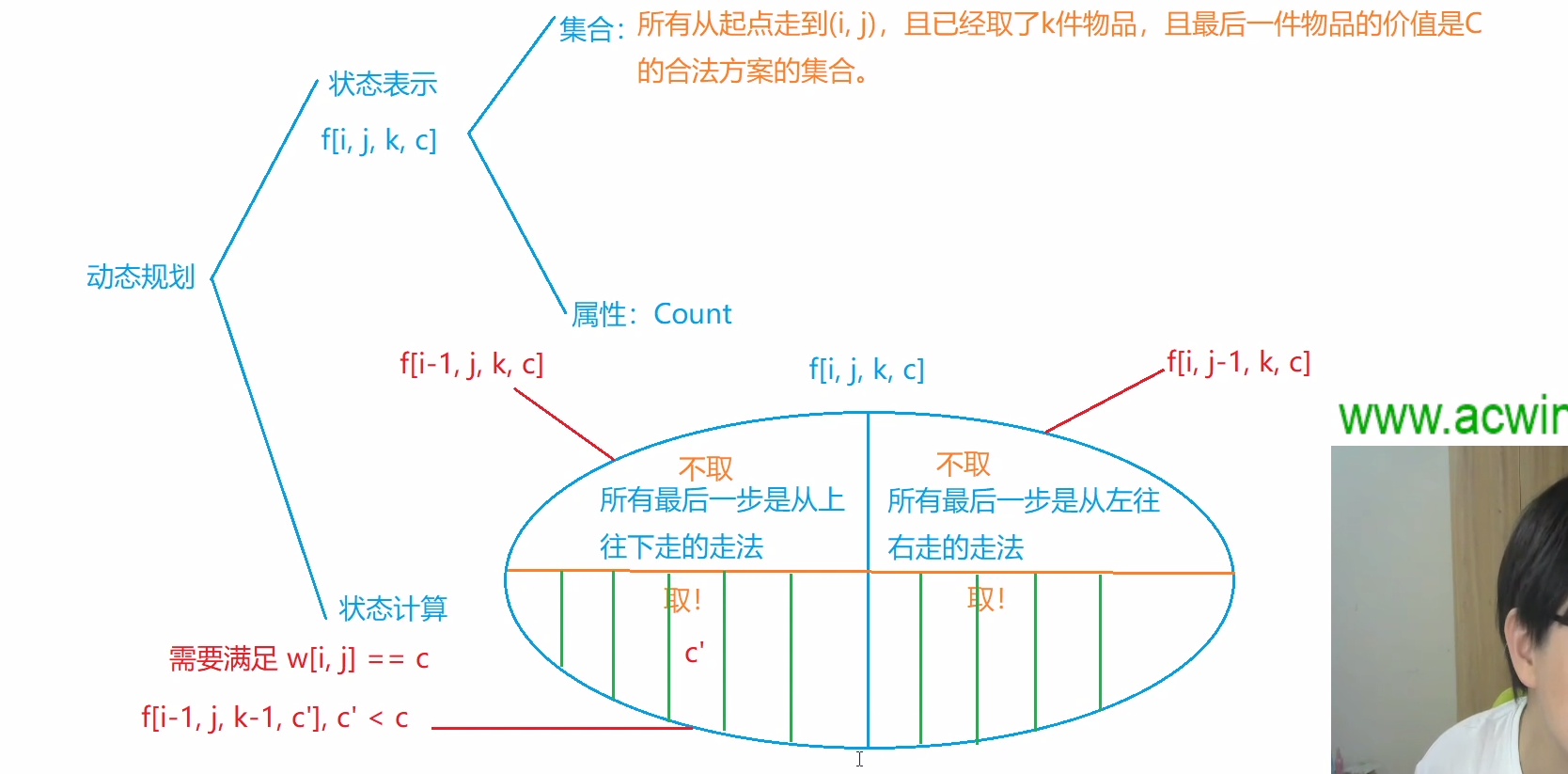
        int[][][][] f=new int[55][55][13][14];//f[i][j][u][v]:表示所有从起点到（i，j),且总共取了u件物品
        int[][] w=new int[55][55];//且最后一件物品的价值是v的合法路线的集合,属性是所有合法路线的总和
        int mod=1000000007;
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=m;j++) {
                w[i][j]=scanner.nextInt();
                w[i][j]++;//在v中规定价值为0时表示不取什么物品，但是物品价值是0~12,为避免冲突需要加一
            }
        }
        f[1][1][0][0]=1;//表示走到第一个物品，且不取第一个物品的方案数为一种
        f[1][1][1][w[1][1]]=1;//表示走到第一个物品，且取第一个物品的方案数为一种
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=m;j++) {
                if(i==1&&j==1)continue;//刚刚已经初始化了不用进行下面操作了，不加这句也行
                for(int u=0;u<=k;u++) {
                    for(int v=0;v<=13;v++) {
                        //由于模很大，不能写f[i][j][u][v]=(f[i][j][u][v]+f[i-1][j][u][v]+f[i][j-1][u][v])%mod;
                        f[i][j][u][v]=(f[i][j][u][v]+f[i-1][j][u][v])%mod;//不取第（i，j）件物品的第一种走法
                        f[i][j][u][v]=(f[i][j][u][v]+f[i][j-1][u][v])%mod;//不取第（i，j）件物品的第二种走法
                        if(u>0&&v==w[i][j]) {//如果要取（i，j）个物品说明物品总数大于等于1件，且最后一件物品是w[i][j]
                            for(int c=0;c<=13;c++) {
                                if(c<w[i][j]) {//若前u-1件的物品的最大价值即c小于w[i][j],则可以取w[i][j]物品
                                    f[i][j][u][v]=(f[i][j][u][v]+f[i-1][j][u-1][c])%mod;//两种走法的取w[i][j]物品表示
                                    f[i][j][u][v]=(f[i][j][u][v]+f[i][j-1][u-1][c])%mod;
                                }
                            }
                        }
                    }
                }
            }
        }
        int res=0;
        for(int i=0;i<=13;i++) {
            res=(res+f[n][m][k][i])%mod;//将所有走到终点，且取了k件物品且最后一件物品价值是i的方案数相加
        }
        System.out.println(res);