题目描述

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

 

示例1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
 

提示：

1 <= arr.length <= 10^5
-100 <= arr[i] <= 100

算法1

(动态规划) $O(n)$

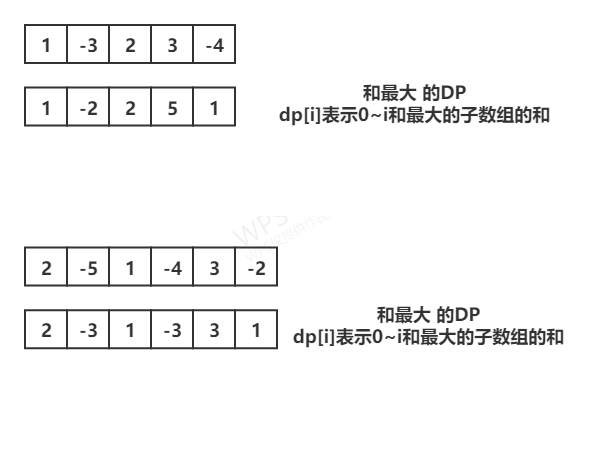
当前0~i的数组中 , nums[i]参与的子数组的最大和，只有两种情况，
1 与前面的子数组的最大和相加， PreMaxSum加上nums[i],
2 不与前面的子数组相加，单独自己成为一个新的子数组。
我们求最大和，那么取两种情况中最大的和.

题目要求的是连续子数组的和，那么PreMaxSum必须也是nums[i-1]参与的数组和的最大值

那么我们定义dp[i] 是当前0~i的数组中,索引为i的数字参与的数组和的最大值

上述情况可以定义为

dp[i] = max(dp[i-1]+nums[i],nusm[i]);

C++ 代码

class Solution {
public:
    int dp[100010];
    int maxSubArray(vector<int>& nums) {
        nums.insert(nums.begin(),0);
        int ans = -9999999;
        for(int i = 1;i<nums.size();i++){
            dp[i] = max(dp[i-1]+nums[i],nums[i]);
            ans = max(ans,dp[i]);
        }

        return ans;
    }
};

我的视频题解空间