题目描述

有一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [u_j, v_j] 表示节点 u_j 和节点 v_j 在树中有一条边。

当 gcd(x, y) == 1，我们称两个数 x 和 y 是 互质的，其中 gcd(x, y) 是 x 和 y 的 最大公约数。

从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。

请你返回一个大小为 n 的数组 ans，其中 ans[i] 是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的，如果不存在这样的祖先节点，ans[i] 为 -1。

样例

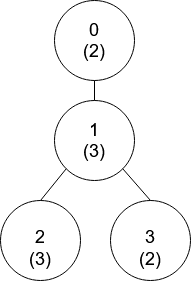
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出：[-1,0,0,1]
解释：上图中，每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。
- 节点 2 有两个祖先节点，分别是节点 1 和节点 0。
    节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，
    所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点，分别是节点 1 和节点 0。
    它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。

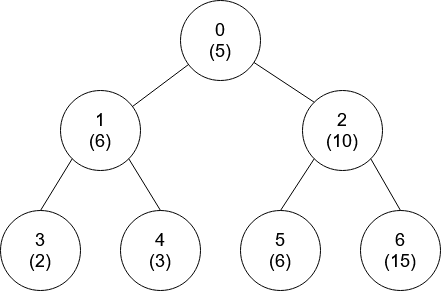
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：[-1,0,-1,0,0,0,-1]

限制

• nums.length == n
• 1 <= nums[i] <= 50
• 1 <= n <= 10^5
• edges.length == n - 1
• edges[j].length == 2
• 0 <= u_j, v_j < n
• u_j != v_j

算法

(深度优先遍历) $O(nS \log S)$

1. 深度优先遍历整棵树，对于每个节点，找到与其互质的所有数字，并更新。
2. 注意，深度优先遍历时，需要记录和恢复现场。

时间复杂度

• 假设最大的数字为 $S$，每个节点需要遍历 $S$ 个数字，每个数字需要 $O(\log S)$ 的时间判定是否互质。
• 故总时间复杂度为 $O(nS \log S)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储树、临时数组、递归调用栈、答案等。

C++ 代码

class Solution {
private:
    vector<int> ans;
    vector<vector<int>> graph;
    vector<int> vis;

    void solve(int u, int fa, const vector<int> &nums) {
        ans[u] = vis[nums[u]];

        vector<int> t(51);
        for (int i = 1; i <= 50; i++) {
            t[i] = vis[i];
            if (__gcd(nums[u], i) == 1)
                vis[i] = u;
        }

        for (int v : graph[u])
            if (v != fa)
                solve(v, u, nums);

        for (int i = 1; i <= 50; i++)
            vis[i] = t[i];
    }

public:
    vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
        const int n = nums.size();
        graph.resize(n);

        for (const auto &e: edges) {
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
        }

        ans.resize(n, -1);
        vis.resize(51, -1);
        solve(0, -1, nums);

        return ans;
    }
};