题目描述

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。

当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是 互质的 ，其中 gcd(x, y) 是 x 和 y 的 最大公约数 。

从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。

请你返回一个大小为 n 的数组 ans ，其中ans[i]是离节点 i 最近的祖先节点且满足nums[i] 和nums[ans[i]] 是 互质的 ，如果不存在这样的祖先节点，ans[i] 为 -1 。

示例 1：

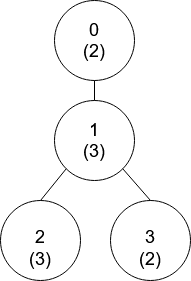
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]] 输出：[-1,0,0,1] 解释：上图中，每个节点的值在括号中表示。 - 节点 0 没有互质祖先。 - 节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。 - 节点 2 有两个祖先节点，分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，所以节点 0 是最近的符合要求的祖先节点。 - 节点 3 有两个祖先节点，分别是节点 1 和节点 0 。它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。

示例 2：

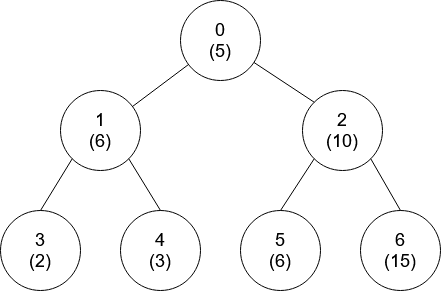
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]] 输出：[-1,0,-1,0,0,0,-1]

提示：

• nums.length == n
• 1 <= nums[i] <= 50
• 1 <= n <= 105
• edges.length == n - 1
• edges[j].length == 2
• 0 <= uj, vj < n
• uj != vj

算法

无向树的 DFS

无向树遍历的套路：dfs 传入一个 father，避免反向遍历

如果直接存祖先路径上所有的数的话，在树是线性的时候复杂度会退化为 $O(N^2)$，我在比赛的时候就被卡在了34/36个测试用例。

但是，这个题目有个很重要的性质，就是 num[i] <= 50，这样在找每个节点的 ans 的时候，可以直接暴力枚举 1~50，看是否互质，如果互质，在最近的哪一层
然后我们用 dep[t] 表示数 t 所在的离当前层的最近的层，-1 表示 t 在祖先中没有存在过
然后我们用 pos[t] 表示满足上述条件的数 t 的节点编号

时间复杂度

$O(50 \cdot N)$

参考文献

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;

int ver[M], Next[M], head[N], tot;
int pos[60], dep[60];
class Solution {
    int n, m;
    vector<int> ans, nums;
    void add(int x, int y) {
        ver[++tot] = y;
        Next[tot] = head[x], head[x] = tot;
    }

    void dfs(int x, int fa, int depth) {
        for (int t = 1; t <= 50; t++) {
            // 如果祖先存在数 t 和 x 互质的话
            if (dep[t] != -1 && __gcd(t, nums[x]) == 1) {
                // 记录 pos 最大，也就是最深的那个祖先
                if (ans[x] == -1 || dep[t] > dep[nums[ans[x]]]) {
                    ans[x] = pos[t];
                }
            }
        }

        int b1 = dep[nums[x]], b2 = pos[nums[x]];
        dep[nums[x]] = depth, pos[nums[x]] = x;
        for (int i = head[x]; i; i = Next[i]) {
            int y = ver[i];
            if (y != fa) dfs(y, x, depth + 1);
        }
        dep[nums[x]] = b1, pos[nums[x]] = b2;
    }

   public:
    vector<int> getCoprimes(vector<int>& _nums, vector<vector<int>>& e) {
        memset(head, 0, sizeof head), tot = 0;
        nums = _nums;
        n = nums.size(), m = e.size();
        ans = vector<int>(n, -1);
        for (auto& t : e) {
            add(t[0], t[1]), add(t[1], t[0]);
        }
        memset(dep, -1, sizeof dep);
        dfs(0, -1, 0);
        return ans;
    }
};