算法1

(区间DP) $O(n^3)$

根据题意可发现其目的是将字母根据频率构建成哈夫曼树，但有一个要求是需要按照字典序构建，可根据一下图片理解题意：

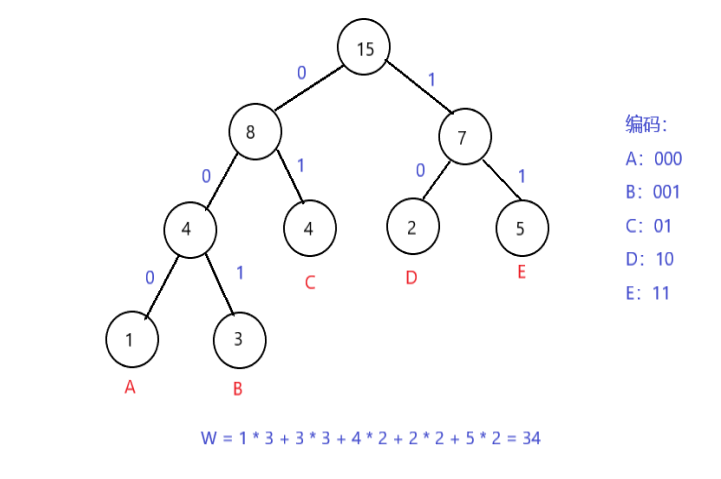
依图可知通过构建字母在树上的位置可以产生不一样的结果，根据哈夫曼左0右1进行编码构造，再根据编码长度求解最后长度。

在此题目中哈夫曼树构造方式即为将相邻的字母或部分进行合并求和，不同合并方式也会产生不一样的结果，因此可以发现和 石子合并 题目完全一致。

状态转移表达式为：

$ F[l, r] = \min\limits_{l \leq k \leq r} \{ F[l, k], F[k + 1, r] \} + \sum_{i=l}^{r}A_i$

时间复杂度

三重循环，一层枚举长度，一层枚举左端点，一层枚举分割点，时间复杂度O($n ^ 3$)

参考文献

石子合并

C++ 代码

#include<iostream>
using namespace std;
const int N = 1010, INF = 0x3f3f3f3f;

int n;
int s[N];
int f[N][N];

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> s[i];
        s[i] += s[i - 1];
    }

    for(int len = 1; len <= n; len ++){
        for(int i = 1; i + len - 1 <= n; i ++){
            int j = i + len - 1;
            if(len == 1) f[i][j] = 0;
            else{
                f[i][j] = INF;
                for(int k = i; k < j; k++){
                    f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
                }
            }
        }
    }
    cout << f[1][n] << endl;
    return 0;
}

算法2

(区间DP + 四边形不等式优化) $O(n^2)$

以下内容均参考于算法进阶指南 和 LYD大佬课程

首先简单阐述一下四边形不等式的含义：

设 $w(x, y) $ 是定义在整数集合上的二元函数，若其定义域上的任意a，b，c, d，其中：$a \leq b \leq c \leq d $ 都有：$ w(a, d) + w(b, c) \leq w(a, c) + w(b + d) $ 成立，则认为该函数满足四边形不等式

观察状态转移方程：

$ F[l, r] = \min\limits_{l \leq k \leq r} \{ F[l, k], F[k + 1, r] \} + \sum_{i=l}^{r}A_i$ 其区间和即满足四边形表达式性质：
下面引入两个定理：

1.

当满足：
1.w满足四边形表达式
2.对于任意的 $a \leq b \leq c \leq d $, $ w(a, d) \geq w(b, c) $
可根据数学归纳法证明F[l, r]也满足四边形表达式性质。(具体证明参考 LYD四边形不等式讲解课或《算法进阶指南》)

2.二维决策单调性：

我们令$p[i, j]$ 为 $F[i, j]$取得最小值的k值
可证明得到：如果$F[l, r]$满足四边形表达式，对于任意的i，j，有$ p[i, j - 1] \leq p[i, j] \leq p[i + 1, j] $ (证明参考如上)

根据上面两则定理，我们可以在 $ p[l, r - 1] \leq k \leq p[l + 1, r] $ 对 k进行枚举，求出$ F[l, r] 和 P[l, r] $

时间复杂度

时间复杂度为：
O$( \sum_{l = 1}^{r} \sum_{r = l + 1}^{N}(p[l + 1, r] - p[l, r - 1] + 1) )$
将该式子的r进行代入，可以得到：
$p[l + 1, l + 1] - p[l, l] + 1 + p[l + 1, l + 2] - p[l, l + 1] + 1 + … $
再将l = l + 1 放入,可得到：
p[l + 1, l + 1] - p[l, l] + 1 + p[l + 2, l + 2] - p[l + 1, l + 1] + 1 + p[l + 1, l + 2] - p[l, l + 1] + 1 + p[l + 2, l + 3] - p[l + 1, l + 2] + 1 + …
可发现公式中几乎消除了一半量，所以最后的时间复杂度优化了一个n级别，为O($n^2$)，这里只是粗略证明，详细证明还有待研究。

参考文献

《算法进阶指南》

C++ 代码

#include<iostream>
#include<cstring>
using namespace std;
const int N = 5010;
int n;
int s[N];
int f[N][N],p[N][N];

int main() {
    cin >> n;
    memset(f, 0x3f, sizeof f);

    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i-1];
        f[i][i] = 0;
        p[i][i] = i;
    }
    for(int len = 2; len <= n; len++)
        for (int l = 1;l + len - 1 <= n; l++) {
            int r = l + len - 1;
            for (int k = p[l][r - 1]; k <= p[l + 1][r]; k++)
                if (f[l][r] > f[l][k] + f[k + 1][r] + s[r] - s[l - 1]) {
                    f[l][r] = f[l][k] + f[k + 1][r] + s[r] - s[l - 1];
                    p[l][r] = k;
                }
        }
    cout<<f[1][n]<<endl;

    return 0;
}