哈夫曼树 和 区间DP 区别

参考:Anoxia_3的题解
附加两幅图, 便于理解

这道题的难点是读懂题, 而不是代码实现

1.首先根据题目中这句话, 想到用哈夫曼树

使得任何一个单词的编码（对应的 01 串）不是另一个单词编码的前缀

2.但是题目又加了这句话, 强制规定了元素顺序, 不让我们使用哈夫曼树简单解决

$a1,a2,…,an$ 的编码是按字典序升序排列的

接着来看看使用哈夫曼树和字典序升序排列得到的答案
1.使用哈夫曼树

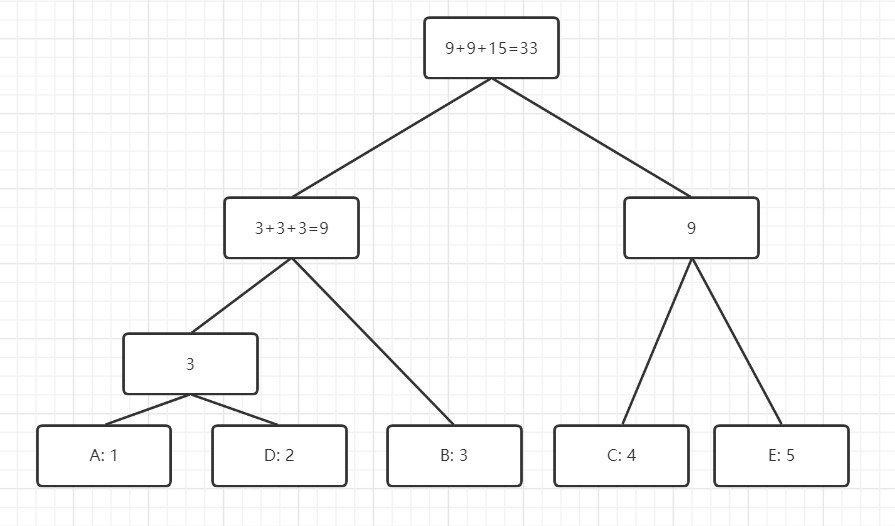
2.使用字典序升序

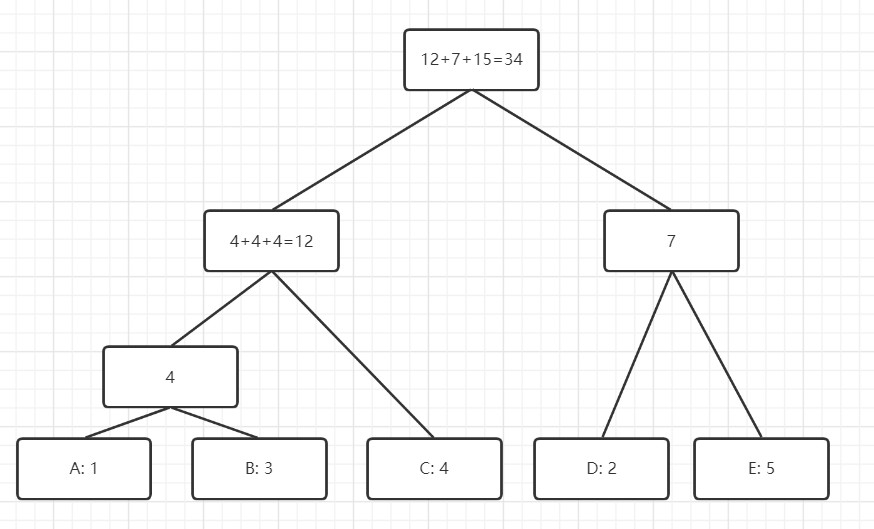
两者的相同点: 每次合并两个节点, 要求最小代价
两者的不同点: 哈夫曼树随意合并, 字典序需要按照顺序合并, 也就是只能合并相邻的两个点

提到只能合并相邻的两个点而且要最小代价, 有没有想到什么?!
没错就是区间DP的模板题:石子合并!

算法: 区间DP

既然看懂了题目的本质, 那就直接套模板
这道题和石子合并的代码一模一样的, 搬过来用就可以
时间复杂度 $O(N^3)$

参考代码

在顺序固定的一排石堆上 每次合并相邻的石堆 求最小代价

化解子问题
最后合并成一堆时 肯定是由两堆合并而来
那就是要让这两堆的代价最小
用f[i][j]表示i~j这一些堆合并起来的最小代价
最终答案就是f[1][n]

用i~k表示左边石堆 k+1~j表示右边石堆
则i~j的最小代价是f[i][j] = min(f[i][k] + f[k+1][j] + sum[i][j])
其中sum[i][j]表示i~j这堆石堆之和 可以用前缀和优化

#include<iostream>
using namespace std;
const int N = 1005;
int sum[N];
int f[N][N];

int main() {
    int n; cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> sum[i];
        sum[i] += sum[i - 1];
    }

    //先枚举区间长度
    //因为合并石堆至少需要两堆 所以区间长度从2开始
    for (int len = 2; len <= n; ++len) {
        //枚举左端点
        for (int l = 1; l + len - 1 <= n; ++l) {
            //确定右端点
            int r = l + len - 1;
            //初始化最大值
            f[l][r] = 1e8;
            //在区间上枚举
            for (int k = l; k <= r; ++k) {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + sum[r] - sum[l - 1]);
            }
        }
    }
    cout << f[1][n];

    return 0;
}