分析

给出两个字符A和B，求A和B最长公共子序列长度以及最长的长度个数有几个。

1. 首先求最长公共子序列

Acwing最长公共子序列
最长公共子序列问题：

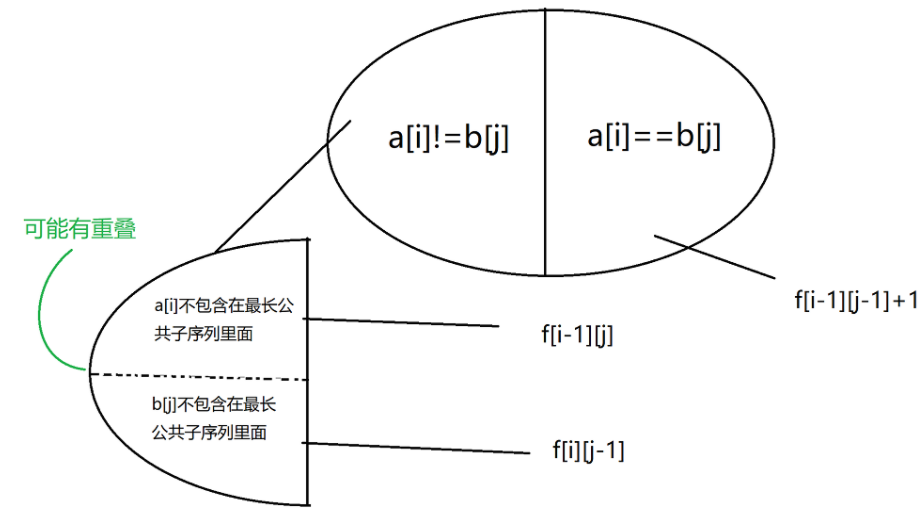
2. 求出了最长的长度，之后要同时把长度的数目计算清楚。

用cnt[i][j]表示A前i位，B前j位的最长公共子序列数目。
对于每个f[i][j]:
1. 若f[i][j]==f[i-1][j],说明状态是从f[i-1][j]转移来的，cnt[i][j]要加上cnt[i-1][j]
2. 若f[i][j]==f[i][j-1],说明状态是从f[i][j-1]转移来的，cnt[i][j]要加上cnt[i][j-1]
3. 若a[i]==b[j]且f[i][j]==f[i-1][j-1]+1,说明状态是从f[i-1][j-1]转移来的，cnt[i][j]要加上cnt[i-1][j-1]
4. 若a[i]!=b[j]且f[i][j]==f[i-1][j-1],那么状态cnt[i-1][j-1]会多加上一次，所以要让cnt[i][j]-=cnt[i-1][j-1]

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N = 5010,mod = 1e8;
int f[2][N],cnt[2][N];  //为防止内存溢出MLE，使用滚动数组，因为每个状态只与上一个状态有关
char s[N],t[N];
int main()
{
    scanf("%s%s",s+1,t+1);
    int n=strlen(s+1)-1,m=strlen(t+1)-1;
    for(int i=0;i<=m;i++)   //初始化，长度为0最长子序列方案数为1（第一个序列长度为0） 
        cnt[0][i]=1;
    cnt[1][0]=1;    //初始化，长度为0最长子序列方案数为1（第二个序列长度为0） 

    for(int i=1;i<=n;i++)
    {
        int now=i&1,pre=now^1;  //当前状态为now,前一个状态为pre
        for(int j=1;j<=m;j++)
        {
            f[now][j]=max(f[pre][j],f[now][j-1]);   //最长公共子序列前两种情况
            cnt[now][j]=0;  //当前状态从上一个状态转移过来的
            if(s[i]==t[j])  
            {
                f[now][j]=max(f[now][j],f[pre][j-1]+1); //最长公共子序列第三种种情况
                if(f[now][j]==f[pre][j-1]+1) cnt[now][j]+=cnt[pre][j-1];     //如果此时满足当前序列f[now][j]等于上一序列f[pre][j-1]+1，cnt当前状态则从上一个状态转移过来
            }
            else
            {
                if(f[now][j]==f[pre][j-1]) cnt[now][j]-=cnt[pre][j-1];  //s[i]!=t[j]并且满足当前序列f[now][j]等于上一序列f[pre][j-1],cnt要减去上一状态的数目，防止重复
            }
            if(f[now][j]==f[pre][j]) cnt[now][j]=(cnt[now][j]+cnt[pre][j])%mod; //状态是从f[i-1][j]转移来的，cnt[i][j]要加上cnt[i-1][j]
            if(f[now][j]==f[now][j-1]) cnt[now][j]=(cnt[now][j]+cnt[now][j-1])%mod; //状态是从f[i][j-1]转移来的，cnt[i][j]要加上cnt[i][j-1]

        }
    }
    printf("%d\n",f[n&1][m]);   
    printf("%d\n",cnt[n&1][m]);
    return 0;
}