题目描述

给定一个数字，我们按照如下规则把它翻译为字符串：
0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。
一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
 

提示：
0 <= num < 2^31

算法1

题目中 每一位的数字是必须要翻译成某一个字母的。
区别在于这一位的数字x是翻译成x对应的字母还是和前面的数字1结合成1x在翻译成对应的字母
或者和前面的数字2结合成2x翻译成对应的字母。

那么如果我们使用
dp[i]表示第i位的数字可以有的翻译方法数目

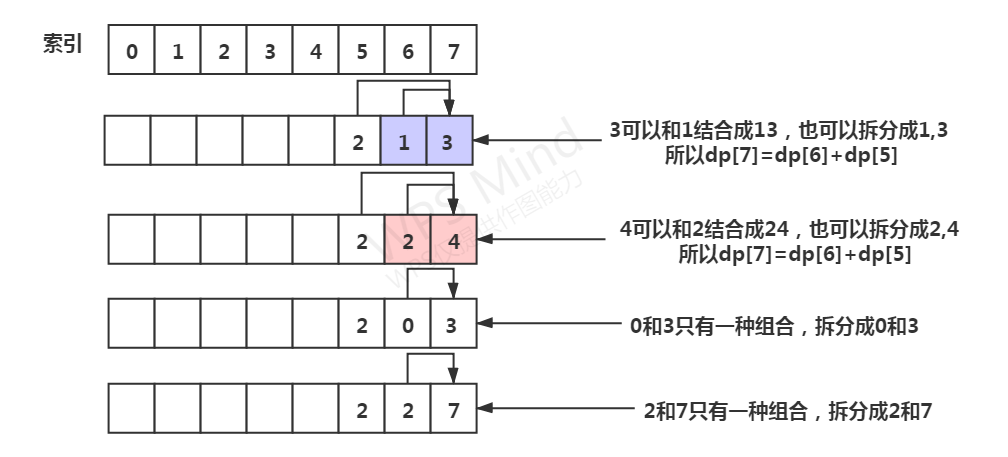
dp[i] = dp[i-1]
或者dp[i] = dp[i-1]+dp[i-2]

取决于i和i-1的数字能否结合成合法的对应的字母
数字1和后面的数字(0~9)均可组合
数字2和后面的数字(0~5)均可组合

C++ 代码

class Solution {
public:
    int dp[100];
    int translateNum(int num) {
        string s = to_string(num);
        dp[0]=1;
        if(s.size()==1) return dp[s.size()-1];
        if(s[0]=='1')dp[1]=dp[0]+1;
        else if(s[0]== '2' && s[1]>='0' && s[1] <= '5') dp[1] = dp[0]+1;
        else{dp[1] =1;}

        for(int i = 2;i<s.size();i++){
            if(s[i-1] == '1') dp[i] =dp[i-1] + dp[i-2];
            else if(s[i-1] == '2' && s[i] >='0' && s[i] <= '5') { cout << 'x'<< endl; dp[i] = dp[i-1]+dp[i-2];}
            else dp[i] = dp[i-1];
        }

        return dp[s.size()-1];
    }
};

我的视频空间