题目描述
在横轴上放了 n 个相邻的矩形,每个矩形的宽度是 1,而第 i(1≤i≤n)个矩形的高度是 hi。
这 n 个矩形构成了一个直方图。
例如,下图中六个矩形的高度就分别是 3,1,6,5,2,3。
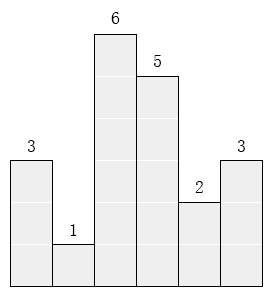
请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。
对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是 10。
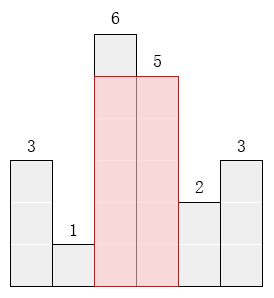
输入格式
第一行包含一个整数 n,即矩形的数量。
第二行包含 n 个整数 h1,h2,…,hn,相邻的数之间由空格分隔。hi 是第 i 个矩形的高度。
输出格式
输出一行,包含一个整数,即给定直方图内的最大矩形的面积。
数据范围
1≤n≤1000,
1≤hi≤10000
输入样例:
6
3 1 6 5 2 3
输出样例:
10
思路
答案的下边界和底边是重合的,因此下边界是不用我们管的,我们是要考虑上,左,右边界就行了
在我们枚举的时候发现,上边界必然和某一个长条的高度是重合的,就是如果我当前的边界没有和任何一个长条的高度重合,那么我的边界就可以往上移,因此我们就可以枚举一下最终结果的上边界是和哪个长条的高度是重合的,一共要枚举n次
还要看一下宽度最大是多少,如果枚举到某一个长条的高度小于当前长条的高度或者找到最后,就停止枚举,最多要把所有的长条都枚举到,所以最多要枚举n次
因此时间复杂度为$O(n^2)$
代码
#include<iostream>
using namespace std;
const int N=1010;
int n;
int h[N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>h[i];
int res=0;
for(int i=1;i<=n;i++)
{
int l=i,r=i;
while(l>=1&&h[l]>=h[i]) l--;
while(r<=n&&h[r]>=h[i]) r++;
res=max(res,h[i]*(r-l-1));//因为到枚举结束,l和r各会向左右走一个,所以应该减去1
//一次题目的图为例,枚举结束后l=2,r=7,而宽度=4,所以宽度就是l-r-1
}
cout<<res;
return 0;
}

