分析

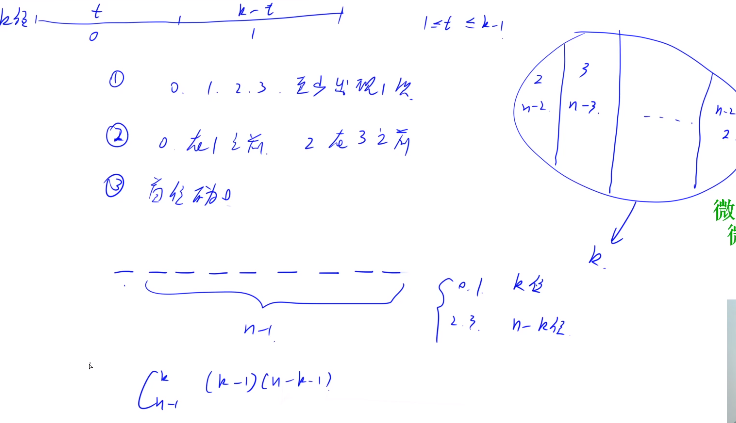
当0,1总个数为k时，第k类的方案数为：
$$ C_{n-1}^{k}(k-1)(n-k-1) $$

将所有的方案累加起来就是最终的答案ans

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+10,mod = 1e9+7;;
typedef long long LL;
int n;
LL ans;
LL qmi(LL a,LL k,LL p)  //快速幂求逆元
{
    LL res=1;
    while(k)
    {
        if(k&1) res=res*a%p;
        a=a*a%p;
        k>>=1;
    }
    return res;
}
int main()
{
    cin>>n;
    for(int i=2;i<=n-2;i++)
    {
        LL C=1;
        for(int j=1,k=(n-1);j<=i;j++,k--)   //计算组合数
        {
            C=(C*k)%mod;
            C=(C*qmi((LL)j,mod-2,mod))%mod;
        }
        ans=(ans+C*(i-1)*(n-i-1))%mod;
    }
    cout<<ans;
    return 0;
}