Acwing 756. 蛇形矩阵

题目链接：

Acwing 756. 蛇形矩阵

例题:

输入样例：

3 3

输出样例：

1 2 3
8 9 4
7 6 5

思路：

误区：

一开始陷入的误区，之前操作二维数组，一般都是一层循环控制行，一层循环控制列。

然后控制的时候一直都是行不变，然后对列进行操作，这样一行一行下去。

甚至都没想到列不变行变来对行进行操作。

可以的操作：

1. 列不变，然后一层循环，对一列进行操作
2. 一层循环直接对行列进行操作（也可以将二维数组看成一维数组）

方法一:一层循环对行列进行全部操作

将二维数组的空间大小作为循环的次数。

一般循环的操作顺序是这样的:

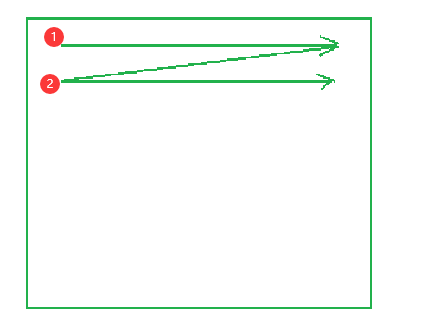
但是这不是我们想要的，我们需要的是像深搜一样，不同的是开头是在左上角，结尾是在最中间而已。

然后搜索的操作是一样的，碰到边界，进行判断，自动转向

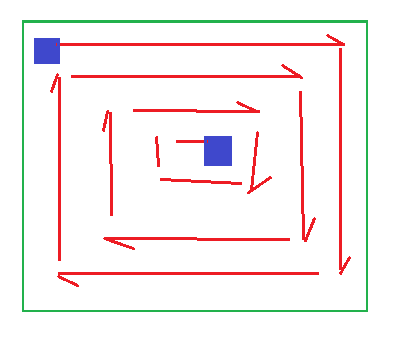
方法二：一行一列的循环操作，直到0

设置四个方向的边界，除非边界的之间的距离为0，说明已经到一个点了。不然就是一行一个循环，一列一个循环，慢慢圈起来

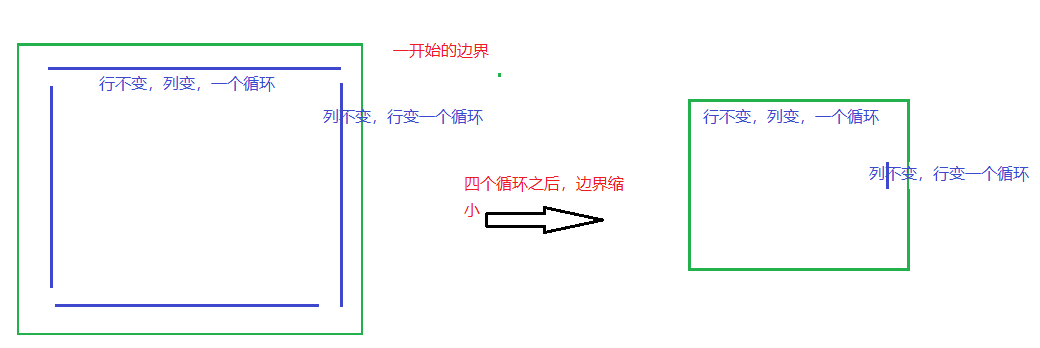
四个循环之后已经走了一环边界缩小，重复下去，直到最后一个点;

代码：方法一

#include<iostream>
using namespace std;
const int N = 105;
// 存放矩阵
int q[N][N];


int main()
{
    int n,m;
    cin>>n>>m;
    // 控制方向，利用循环跟判断控制方向，上右下左
    int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1},d = 1;

    // 控制行走的坐标
    int x = 0,y = 0;

    // 模拟蛇在走，总共走n*m格
    for(int i = 1; i <= n*m; i++)
    {
        // 赋值
        q[x][y] = i;
        // 将下一步的坐标赋值给a,b
        int a = x + dx[d],b = y + dy[d];
        // 判断如果碰壁，
        if(q[a][b] != 0 || a >= n || b >= m || a < 0 || b < 0)
        {
            d = (d+1) % 4;

            a = x + dx[d],b = y + dy[d];
        }

        x = a, y = b;
    }

    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
            cout<<q[i][j]<<' ';
        cout<<endl;


    return 0;
}