图论的题目 显然最重要的就是先建图 以样例为例 建图方式如下图所示:

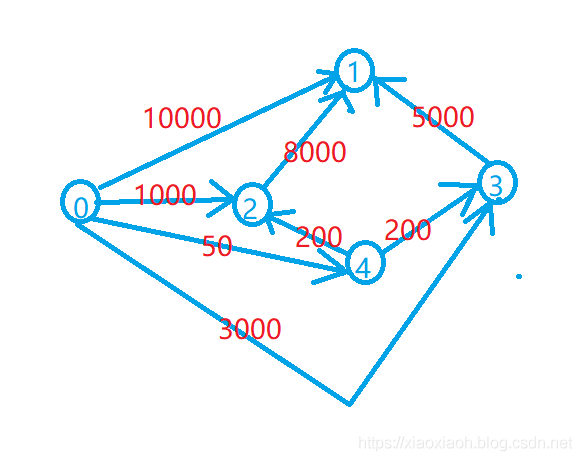
那么是如何想到这样的构图方式呢??
作为最短路 先找起点和终点
终点显然就是酋长的允诺编号为1 那么起点该是什么呢??
显然起点我们是不确定的 因此我们想到了构建一个虚拟的原点 寻找从虚拟原点到1的”最短路径”
交换物品的花费作为边权 求最小的花费就变成了求最短路径
那么等级的问题该怎么解决呢 酋长的等级是level[1] 那么要与酋长进行交换的话必然是在
level[1]-m~level[1]+m间的某个长度为m的区间 因为要么一直都是高 要么一直是低
我们暴力枚举每一个等级区间 找在各个区间中的最小值 那么便可以求得答案了

C++ 代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=110;
int dist[N];
int level[N];
int w[N][N];
bool st[N];
int n,m;

int dijkstra(int down, int up)//dijkstra的模板
{
    memset(dist, 0x3f, sizeof dist);
    memset(st,false,sizeof st);//一定要初始化 
    dist[0] = 0;
    for (int i = 1; i <= n + 1; i ++ )
    {
        int t = -1;
        for (int j = 0; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t=j;
        st[t] = true;
        for (int j = 1; j <= n; j ++ )
            if (level[j] >= down && level[j] <= up)//控制等级范围
                dist[j] = min(dist[j], dist[t] + w[t][j]);//更新距离
    }
    return dist[1];
}


int main()
{
    cin>>m>>n;//m是等级差限制 n种物品
    memset(w,0x3f,sizeof w);
    for(int i=1;i<=n;i++) w[i][i]=0;//自己对自己不花钱

    for(int i=1;i<=n;i++)
    {
        int price,cnt;
        cin>>price>>level[i]>>cnt;//每种物品的价格 对应的的等级 替代物品的数量
        w[0][i]=min(w[0][i],price);//假设虚拟原点为0号点  即直接买的话就是他的price
        while(cnt--)
        {
            int id,cost;
            cin>>id>>cost;//每个替代物品对应的编号和花费(即图上的的权重)
           w[id][i]=min(w[id][i],cost);//更新一下权重
        }
    }
    int res=0x3f3f3f3f;
    for(int i=level[1]-m;i<=level[1];i++) res=min(res,dijkstra(i,i+m));//枚举level[1]-m~level[1]+m 内的所有区间 每个区间都查一次

    cout<<res<<endl;
    return 0;
}

感谢xxh的图片