枚举回溯

1.解题思路

对每个位置的两种情况进行枚举 :

• 不在当前位置 放置皇后，这种情况下会直接调用下一次dfs()函数。
• 当判断条件通过时，在当前位置放置皇后，并调用下一次dfs()函数。记得在调用dfs()函数之后，进行现场的恢复。

2.Question && Answer

dfs()函数中的 dg 和 udg 数组是怎么当做判断条件的？

将棋盘当作一个二维坐标系，原点在左下角，如下图 :

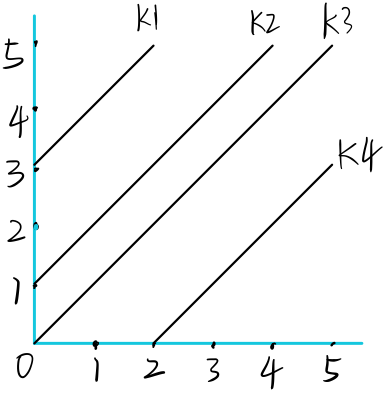
首先先将题干中所说的两个皇后不能再同一斜线上，可以理解为两个皇后不能在同一条对角线上。
然后, 我们用dg[i] 数组表示每一条 正 对角线(原因如下段), udg[i] 同理。随着i的不同表示不同的对角线。
我们用 bool 类型的 dg[i] 数组存储正对角线上是否有皇后存在的状态。若存在皇后赋值为 true, 不存在赋值为 false。
当 !dg[i] 成立时, 表示 dg[i] = false, 即此条对角线上可以放置皇后。

下面是 dg[i] 数组能与正对角线（即斜率大于0）一一对立的原理 :
可以看到在上图 5$\ast$5 的坐标系中,斜率大于 0 的对角线共有 2$\ast$5-1 条,反对角线同理。
我们使用截距 b 来表示每一条对角线。
如上图中的对角线k2, 我们可以用它的截距 1 来表示这条对角线，
这样, 斜率大于 0 的对角线就可以用 dg[-4] 到 dg[4] 表示每一条对角线，
这样很明显可以看到数组索引为负数越界, 所以我们将每条截距的值加上 n ,即用 dg[5+1=6] 来表示截距为 1 的对角线 k2。
这样就能理解在代码中的 !dg[n+y-x] 了。

码字好累 OwO

3.AC代码

import java.util.*;
import java.io.*;

class Main{
    private static int n = 0;
    private static boolean[] dg, udg, col, row;
    private static char[][] g;

    public static void main(String[] args)  throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(in.readLine());
        dg = new boolean[2 * n]; udg = new boolean[2 * n];
        col = new boolean[n]; row = new boolean[n];
        g = new char[n][n];
        dfs(0, 0, 0);
    }

    static void dfs(int x,int y, int s){
        if(s > n)   return ;
        if(y == n){
            y = 0;
            x ++;
        }  
        if(x == n){
            if(s == n){
                for(int i = 0;i < n;i ++)   System.out.println(g[i]);
                System.out.println();
            }
            return ;
        }

        //不在当前位置放置皇后
        g[x][y] = '.';
        dfs(x, y + 1, s);

        //在当前位置放置皇后
        if(!row[x] && !col[y] && !dg[n+y-x] && !udg[x+y]){
            row[x] = col[y] = dg[n+y-x] = udg[x+y] = true;
            g[x][y] = 'Q';
            dfs(x, y+1, s+1);
            g[x][y] = '.';
            row[x] = col[y] = dg[n+y-x] = udg[x+y] = false;
        }
    }

    static void graph_print(){
        for(int i = 0;i < n;i ++){
            for(int j = 0;j < n;j ++){
                System.out.print(g[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println();
    }
}