题目描述

原题

给定 n 个区间 [li,ri]，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：[1,3]和[2,6]可以合并为一个区间[1,6]。

输入格式
第一行包含整数n。

接下来n行，每行包含两个整数 l 和 r。

输出格式
共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围
1≤n≤100000,
−109≤li≤ri≤109

输入样例：
5
1 2
2 4
5 6
7 8
7 9
输出样例：
3

算法：模拟 + 贪心

思路：
1.先把所有区间的左端点进行排序。（这是为了后面遍历的时候，减少一种区间关系：下一个的区间左端点比当前这个区间的左端点还要小）
2.排完序后就可以对区间进行合并了。合并也很简单，就是比较下一个区间的左端点跟当前这个区间的右端点进行比较，如果下一个区间的左端点大于当前区间的右端点的话，那就说明这两个区间没有交集，直接把当前这个区间加入到数组去，如果小于，说明这两个区间有交集，此时选取较大的左端点，更新。
3.遍历结束后，也就完成了区间合并。
（详情见代码注释）

区间左端点排完序之后的区间关系：

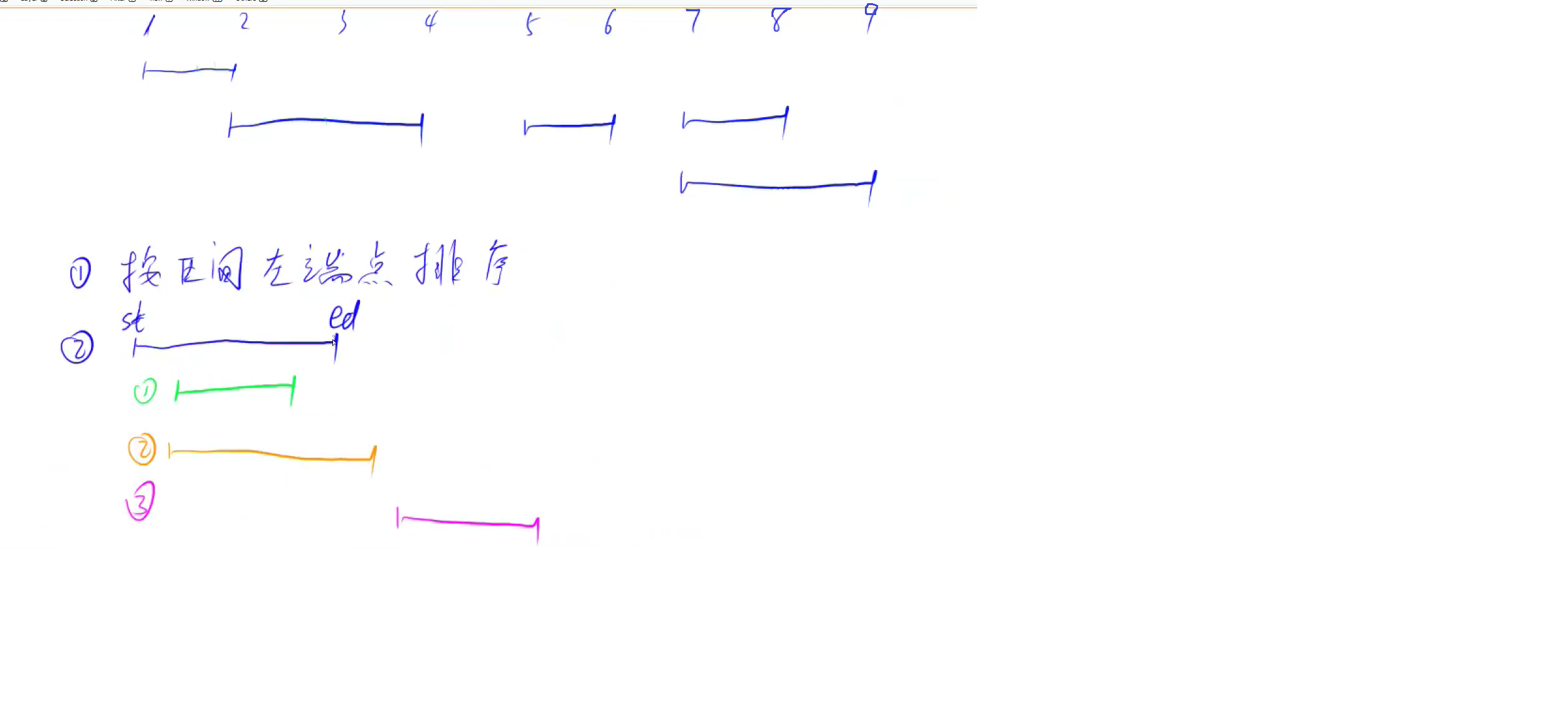
（来源y总视频）

参考文献

y总讲解视频

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 100010;
//每个区间都有左右两个端点，我们用pair类型来表示
typedef pair<int,int> PII;
//存储每个区间的端点，类型是pair
vector<PII> segs;

//把给定的区间合并成没有交集的区间
void merge(vector<PII> &segs){
    //定义个临时存放答案的
    vector<PII> res;
    //先对每个区间的左端点进行排序
    sort(segs.begin(),segs.end());
    //定义个两个临时区间端点，用于比较，初始值定为负无穷
    int start = -2e9 , end = -2e9 ; 
    //遍历每个区间
    for(auto seg : segs){
        //遍历的下一个区间跟当前这个区间没有交集的话
        if(end < seg.first){
            //这里的这个判断是防止把最开始自己定义无穷大的区间给放进去
            if(start != -2e9) res.push_back({start , end});
            //然后更新一下下一个新的区间的左右端点
            start = seg.first , end = seg.second;
        }
        else{//如果有交集的话
        //那我们就需要把当前的这个区间右端点更新为较大的那个，合并掉
            end = max(end , seg.second);
        }
    }
    //最后把最后一个没有放进去的区间给加入到vector中，这个判断主要是防止
    //空区间输入的是
    if(start != -2e9) res.push_back({start,end});
    //最后更新到答案vector中
    segs = res;

}

int main(){
    //输入n
    int n;
    cin>>n;
    for(int i = 0 ; i < n ; i++){
        int l , r;
        cin >> l >> r;
        //把n对区间放到vector中
        segs.push_back({l,r});

    }
    merge(segs);
    //输出合并后的区间个数
    cout<<segs.size()<<endl;
    return 0;
}