01分数规划问题

步骤：
1. 确认答案区间，然后二分，判断性质
2. 借助上述二分出的中点，推导出性质的公式
3. 套用图论模板算法

本题首先我们要求的是在一个环内 $\frac{\sum f(i)}{\sum t(i)}$ 的最大值

这个答案本身具有二分的性质【存在标准大于等于k的环 | 不存在】，我们就是要二分到他的最大值

根据数据范围可以推断出答案是在 $[1, 1000]$ 上的浮点数二分问题

利用二分出的mid，我们有公式 $\frac{\sum f(i)}{\sum t(i)} > mid$ ，对公式进行变形

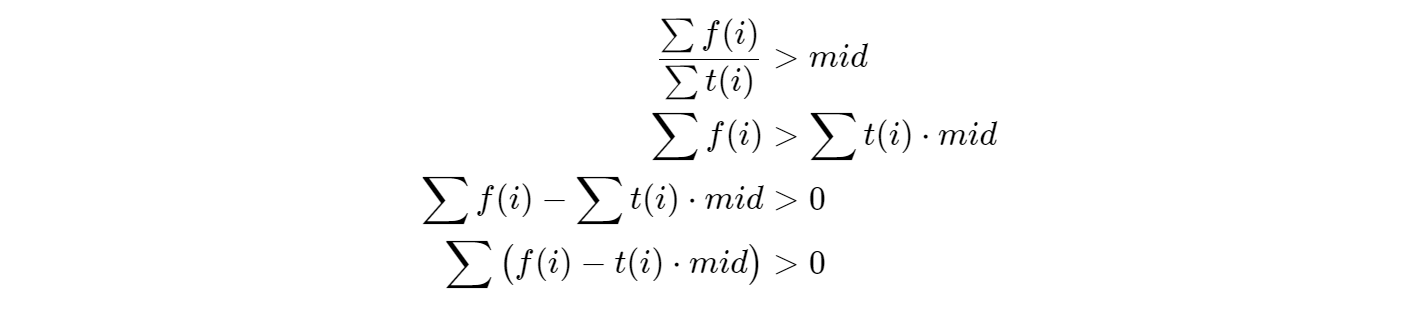
根据上述推导的公式，我们可知，满足要求mid，就是要满足图中存在一个环，他的 $\sum \big( f(i) - t(i) \cdot mid \big) > 0$

spfa算法本身具有一个性质，就是在求解最短路的时候，是可以把点权和边权看做一个整体边权一起更新的，因此我们常常在一些spfa的图论问题中，把点权存入边权中进行计算。

这题我们就要利用到spfa的性质，把边权 $t(i)$ 换成 $f(i) - t(i) \cdot mid$ 来存储，把每个点的权值存入他的出边中

这样，原问题就转换成了求一个图中是否存在一个正环的问题了

求图中是否存在正环，和求负环是一个对称问题，直接更改spfa算法中的不等号方向，转而变成求最长路算法中是否存在正环，即可办到

本题代码：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 5010;
const double eps = 1e-4;

int n, m;
int w_ver[N];
int h[N], e[M], w_edg[M], ne[M], idx;
double dist[N];
int cnt[N], q[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w_edg[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
bool check(double limit) {
    memset(dist, 0, sizeof dist);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);

    int hh = 0, tt = 0;
    for (int i = 1; i <= n; ++i) {
        q[tt++] = i;
        st[i] = true;
    }

    while (tt != hh) {
        int t = q[hh++];
        if (hh == N) hh = 0;
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            //这里求是否存在正环，因此spfa从寻找“最短路”改为寻找“最长路”
            if (dist[j] < dist[t] + w_ver[t] - limit * w_edg[i]) {
                dist[j] = dist[t] + w_ver[t] - limit * w_edg[i];
                cnt[j] = cnt[t] + 1;

                if (cnt[j] >= n) return true;

                if (!st[j]) {
                    st[j] = true;
                    q[tt++] = j;
                    if (tt == N) tt = 0;
                }
            }
        }
    }
    return false;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", &w_ver[i]);

    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    double l = 1, r = 1000;
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (check(mid)) l = mid;
        else r = mid;
    }
    printf("%.2lf\n", l);
    return 0;
}