AcWing 831. KMP字符串

看别人写题解很简单，自己写真的很难，有错误请大佬一定指正，Orz

题目描述

给定一个模式串S，以及一个模板串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串P在模式串S中多次作为子串出现。

求出模板串P在模式串S中所有出现的位置的起始下标。

输入格式

第一行输入整数N，表示字符串P的长度。

第二行输入字符串P。

第三行输入整数M，表示字符串S的长度。

第四行输入字符串S。

输出格式

共一行，输出所有出现位置的起始下标（下标从0开始计数），整数之间用空格隔开。

输入样例

3
aba
5
ababa

输出样例

0 2

算法1

Brute Force（暴力）

C++ 代码

#include <iostream>

using namespace std;

int n, m;
char s[1000010], p[100010];

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++ )cin >> p[i];
    cin >> m;
    for(int i = 0; i < m; i ++ )cin >> s[i];

    for(int i = 0; i < m; i ++ )
    {
        bool flag = true;
        for(int j = 0; j < n; j ++ ) 
        {
            if(s[i + j] != p[j]) 
            {
                flag = false;
                break;
            }        
        }
        if(flag) cout << i << ' ';
    }
    return 0;
}

很显然，会超时

只能过12个数据

因此，暴力是不行的，所以要祭出我们的KMP大法！！！

算法2

KMP算法

萌新第一次写题解，只是感觉KMP算法太难了，怕自己忘记，因此边学边写的，如果有错误，还请大佬指正^ - ^

一、KMP算法的简介

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

二、KMP算法的优点

KMP算法最大的优点应该就是优于暴力做法。

三、时间复杂度 $ O(m + n) $

四、参考文献

算法基础课
大佬的题解

五、算法理解

首先要理解几个基本概念
1.前缀：除最后一个字符外，字符串的前部集合

2.后缀：除第一个字符外，字符串的后部集合

3.next[i]数组的含义：是以i为终点的后缀和从1开始的前缀相等且后缀的长度最长的数组(即最长相等子前后缀的长度)

六、算法解释

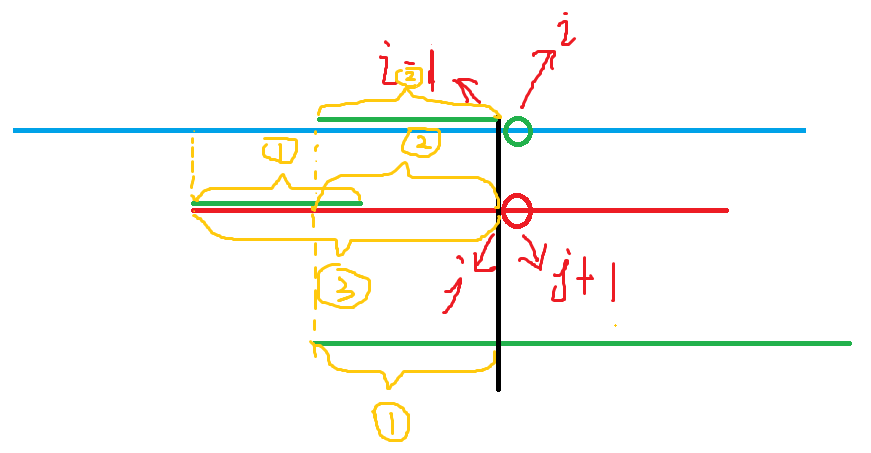
1串为：[1, next[j]]
2串为：[j - next[j] + 1,j]

当图中的s[1, i - 1] == p[1, j] && s[i] != p[j + 1]时，说明黑线以前的3号串都是匹配的，而s[i] != p[j + 1]， 说明黑线以后不匹配，需要将p[]串往后移动（不止移动一位，移动到下次能够匹配的地方），由图可知此时1串等于2串，所以移动到图中的红线下面的绿线所在位置，这个步骤可由j = next[j]完成，直到s[i] == p[j + 1]时，将j ++ ，直到j == n时说明匹配成功。

附上代码

for(int i = 1, j = 0; i <= m; i ++ )
    {
        while(j && s[i] != p[j + 1]) j = ne[j];
        // 当s[]串的s[i] != p[j + 1]时，说明s[]串与p[]串不匹配
        // 需要将j移动到ne[j]的位置
        if(s[i] == p[j + 1]) j ++ ;
        if(j == n) 
        {
            cout << i - n << ' ';
            j = ne[j];
        }
    }

所以，我们的重点转向如何求next[]。

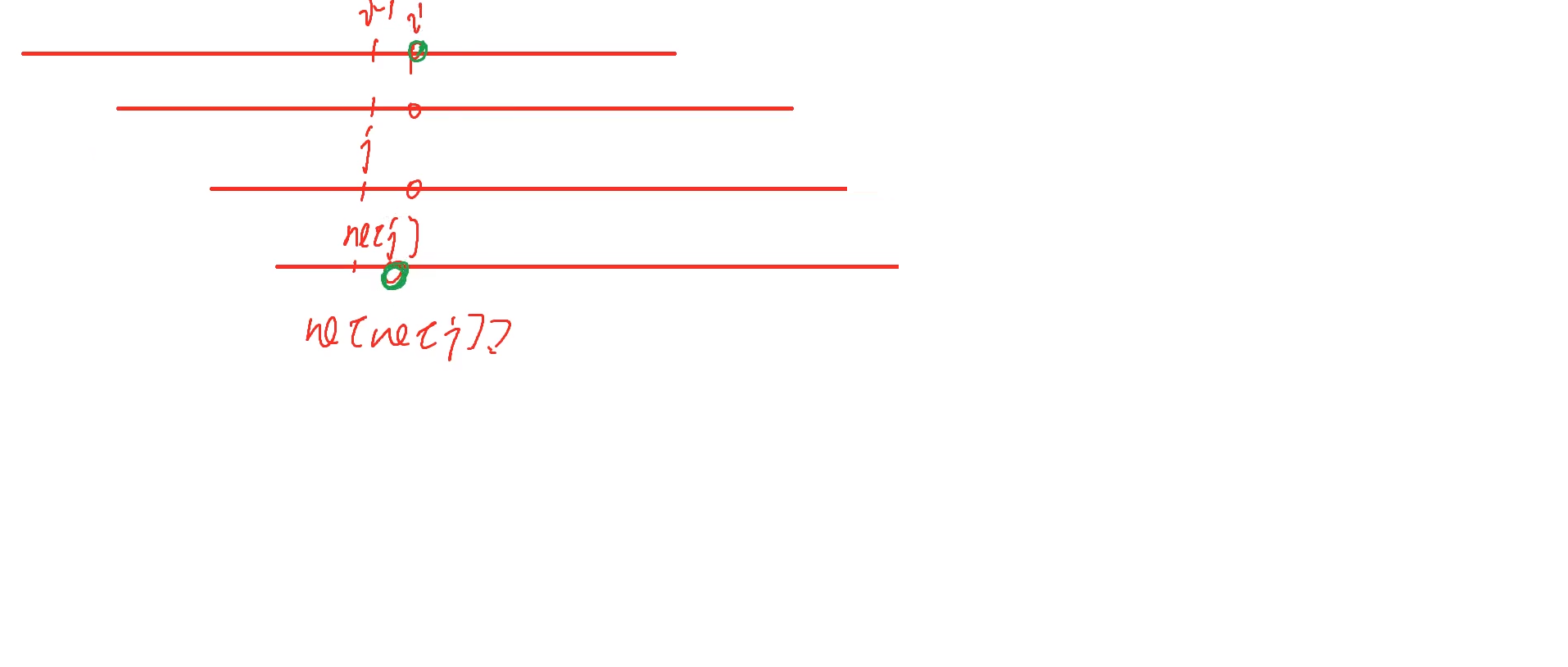
这里盗用y总的图片，不想自己画图了QAQ

先附上代码

for(int i = 2, j = 0; i <= n; i ++ )
    {
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

可以发现，与前面KMP匹配的过程极其相似，相当于p[]与p[]自身匹配。

区别就是在每次移动j时，将j输入到next[]中。

七、C++ 完整代码

#include <iostream>

using namespace std;

const int N = 100010, M = 1000010;

int n, m;
int ne[N];
char s[M], p[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;

    // 求next[]过程
    for(int i = 2, j = 0; i <= n; i ++ )
    {
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

    // KMP匹配过程
    for(int i = 1, j = 0; i <= m; i ++ )
    {
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) j ++ ;
        if(j == n) 
        {
            cout << i - n << ' ';
            j = ne[j];
        }
    }
    return 0;
}