3208. Z字形扫描

在图像编码的算法中，需要将一个给定的方形矩阵进行 $Z$ 字形扫描(Zigzag Scan)。

给定一个 $n×n$ 的矩阵，$Z$ 字形扫描的过程如下图所示：

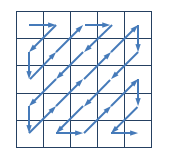
对于下面的 $4×4$ 的矩阵，

1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

对其进行 $Z$ 字形扫描后得到长度为 $16$ 的序列：1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3。

请实现一个 $Z$ 字形扫描的程序，给定一个 $n×n$ 的矩阵，输出对这个矩阵进行 $Z$ 字形扫描的结果。

输入格式
输入的第一行包含一个整数 $n$，表示矩阵的大小。

输入的第二行到第 $n+1$ 行每行包含 $n$ 个正整数，由空格分隔，表示给定的矩阵。

输出格式
输出一行，包含 $n×n$ 个整数，由空格分隔，表示输入的矩阵经过 $Z$ 字形扫描后的结果。

数据范围
$1≤n≤500，$
矩阵元素为不超过 $1000$ 的正整数。

输入样例：

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

输出样例：

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

思路：

众所周知，一个二维矩阵一共有 $2n-1$ 条正对角线和 $2n-1$ 条副对角线。
而这里我们发现扫描都是沿着副对角线走的，下图便是扫描一个$5 × 5$ 矩阵的图示：

我们发现扫描可以分为两个方向，右上和左下。

又因为$n×n$的矩阵，副对角线都是45度，即斜率是1，因此我们有y = x + b; 即x - y = b;其中b是截距，是固定不变的，也就是说，副对角线的坐标之差是固定的。

因此可以利用这个关系来算坐标。

此外，当我们给上图中的2n - 1 条对角线从0 ~ 2n - 2编号时，会发现偶数编号的对角线是往右上走的，而奇数编号的对角线是往左下走的,如下图：

当然，我们在扫描的时候，还应该保证下标没有越界。

Java代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] arr = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                arr[i][j] = sc.nextInt();
            }
        }

        //注意这里i表示的是当前遍历的是第几条副对角线，而非横坐标，共2n - 1条副对角线
        for (int i = 0; i <= 2 * n - 1; i++) { 
            if ((i & 1) == 0) {//第偶数条对角线往右上走
                for(int j = i; j >= 0;j--){//j表示当前副对角线起点的横坐标，纵坐标由i - j算出即可
                    if (j >= 0 && j < n && i - j >= 0 && i - j < n) { //坐标越界检查
                        System.out.print(arr[j][i - j] + " ");
                    }
                }
            }else{//第奇数条对角线往左下走
                for (int j = 0; j <= i; j++) {//j表示当前副对角线起点的横坐标，纵坐标由i - j算出即可
                    if (j >= 0 && j < n && i - j >= 0 && i - j < n) { //坐标越界检查
                        System.out.print(arr[j][i - j] + " ");
                    }
                }
            }
        }
    }
}