5.2 差分

查分是前缀和的逆运算

原数组：a：a[1], a[2], a[3], ... , a[n];

构造一个差分数组：b ： b[1], b[2], b[3], ... , b[n];

使得: a[i] = b[1] + b[2]+ b[3] + … + b[i];

即：a是b的前缀和数组， b是a的差分数组。

构造差分数组：

a[0] = 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] = a[3] - a[2];

......

b[i] = a[i] - a[i-1];

可反推：a[3] = b[1] + b[2] + b[3] = a[1] -a[0] + a[2] - a[1] + a[3] - a[2] = a[3] ;

证明a是b的前缀和数组

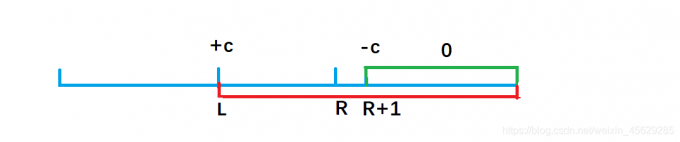
问题: 令数组a的区间[l, r]的元素，全部加上c

由于b是a的差分数组，所以：

1. 若b[1] + c, 则a中1…N都会加上c
2. 若b[l] + c, 则a中l…N也都会加上c
3. 若b[1] - c, 则a中1…N都会减去c
4. 若b[r+1] - c, 则a中r+1…N也都会减去c // 将后面多加的减去
5. 即: b[l] += c; b[r +1] -= c;

注：此图为借

#include <iostream>
using namespace std;
const int n = 100010;
int a[n], b[n];
int main()
{
    int N, K;
    cin >> N >> K;

    // 构造差分数组
    for (int i = 1; i <= N; i++)
        cin >> a[i], b[i] = a[i] - a[i - 1];
    while (K--)
    {
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;
        b[r + 1] -= c;
    }
    // 还原数组
    for (int i = 1; i <= N; i++)
        b[i] += b[i - 1], cout << b[i] << " ";

    return 0;
}