题目描述

在一个定义了直角坐标系的纸上，画一个 (x1,y1) 到 (x2,y2) 的矩形指将横坐标范围从 x1 到 x2，纵坐标范围从 y1 到 y2 之间的区域涂上颜色。

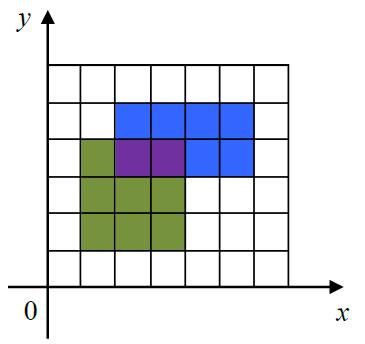
下图给出了一个画了两个矩形的例子。

第一个矩形是 (1,1) 到 (4,4)，用绿色和紫色表示。

第二个矩形是 (2,3) 到 (6,5)，用蓝色和紫色表示。

图中，一共有 15 个单位的面积被涂上颜色，其中紫色部分被涂了两次，但在计算面积时只计算一次。

在实际的涂色过程中，所有的矩形都涂成统一的颜色，图中显示不同颜色仅为说明方便。

给出所有要画的矩形，请问总共有多少个单位的面积被涂上颜色。

输入格式

输入的第一行包含一个整数 n，表示要画的矩形的个数。

接下来 n 行，每行 4 个非负整数，分别表示要画的矩形的左下角的横坐标与纵坐标，以及右上角的横坐标与纵坐标。

输出格式

输出一个整数，表示有多少个单位的面积被涂上颜色。

数据范围

1≤n≤100,

0≤ 横坐标、纵坐标 ≤100

输入样例：

2
1 1 4 4
2 3 6 5

输出样例：

15

思路

此题如果想做出$O(nlogn)$的效果，可以自行查一下扫描线

如果只想平平安安地过了这道题，莫慌，可以模拟

因为数据范围最多是100，所以我们可以把整个区间分成10000个格子，然后给每一个格子编上编号

这道题最多可能会有100个矩形，每个矩形最多会有10000个格子，所以这道题的时间复杂度最大为$10^6$，直接模拟即可

只有在数据范围特别大的时候我们才考虑要不要使用更加优化的算法

代码

#include<iostream>
using namespace std;
bool st[110][110];
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        //我们在编号的时候x1,y1对应的格子坐标是(x1,y1),x2,y2对应的格子坐标是(x2-1,y2-1) 
        //因为每个格子的编号是它的左下角坐标 
        for(int i=x1;i<x2;i++)
        {
            for(int j=y1;j<y2;j++)
            {
                st[i][j]=1;
            }
         } 
    }
    int res=0;
    for(int i=0;i<110;i++)
    {
        for(int j=0;j<110;j++)
        {
            if(st[i][j]==1)
                res++;
        }
    }
    cout<<res;
    return 0;
}