AcWing 1351. 密码锁（两个圆环容斥原理）    原题链接    简单

作者： 作者的头像   wide ,  2021-02-26 16:50:04 ,  所有人可见 ,  阅读 2060

25


3

公式求解：容斥原理

时间复杂度 $O(1)$

思路

题意是给定两个3位密码(类比两把锁)且相差2以内的数可选。

思路是锁1可选数+锁2可选数-锁1锁2公共可选数。

注意点：

计算可选数时一定是要考虑拨盘总数n ！！！

1、计算锁1/锁2分别可选数：

  • 情况一：当不受限于拨盘总数n，即n > 5：
    锁1：A-2~A+2;B-2~B+2;C-2~C+2
    锁2：D-2~D+2;E-2~E+2;F-2~F+2
    所以锁1可选数：5 * 5 * 5，锁2可选数：5 * 5 * 5

  • 情况二：当受限拨盘总数n，即n <= 5，给定的3位密码也一定在n以内,此时可选数为1~n
    所以锁1可选数：n * n * n，锁2可选数：n * n * n
    综上，single = 锁1/锁2可选数：Math.min(n,5) * Math.min(n,5) * Math.min(n,5)

2、计算锁1锁2公共可选数

  • 先计算锁1和锁2密码相同位上数的距离d:
    一般情况下两数之间距离为Math.abs(a - b)
    但是在圆环中当a和b的距离太远，则需要取如图a和b反向的那段较小的距离，即n - Math.abs(a - b)
    因此，d = Math.min(Math.abs(a[i] - b[i]),n - Math.abs(a[i] - b[i]))
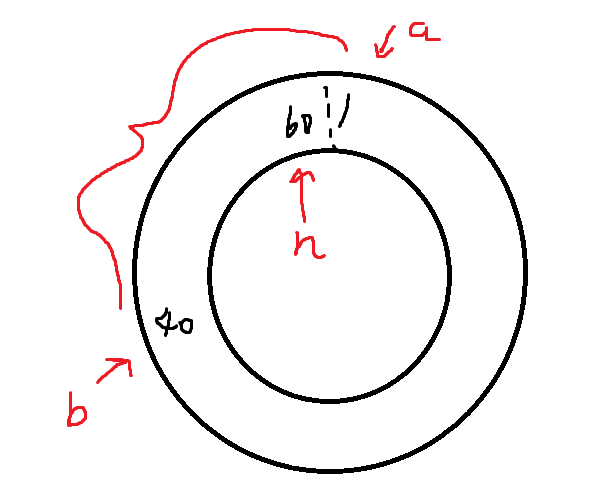
    QQ截图20210226152824.png

  • 情况一：当不受限于拨盘总数n，即n > 5：
    枚举可得规律：
    当d > 5，公共可选数0；当d <= 5，公共可选数5 - d
    所以每一位上的公共可选数为：Math.max(0,5-d)

  • 情况二：当受限拨盘总数n，即n <= 5:
    所以每一位上的公共可选数为n

综上：锁1锁2公共可选数为：
both = Math.min(Math.max(0,5-d1),n) * Math.min(Math.max(0,5-d2),n) * Math.min(Math.max(0,5-d3),n)

最终答案为single * 2 - both

Java 代码

import java.util.*;
public class Main{
    static int[] a = new int[3];
    static int[] b = new int[3];
    static int n;
    public static int both(){
        int res = 1;
        for(int i = 0;i < 3;i++){
            int d = Math.min(Math.abs(a[i] - b[i]),n - Math.abs(a[i] - b[i]));
            int r = Math.min(n,Math.max(0,5 - d));
            res *= r;
        }
        return res;
    }
    public static int single(){
        int res = 1;
        for(int i = 0;i < 3;i++){
            res *= Math.min(n,5);
        }
        return res;
    }
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for(int i = 0;i < 3;i++){
            a[i] = sc.nextInt();
        }
        for(int i = 0;i < 3;i++){
            b[i] = sc.nextInt();
        }
        int res = single() * 2 - both();
        System.out.println(res);
    }
}

暴力枚举

时间复杂度$O(n^3)$

注意点：

所求答案的三位必须与锁1上的三位数对应满足 或 与锁2上的三位数对应满足，
而不是答案的某几位和锁1对应的那几位满足，而其他位和锁2的对应位满足！

Java 代码

import java.util.*;
public class Main{
    static int[] a = new int[3];
    static int[] b = new int[3];
    static int n;
    static int cnt;
    //检查i 与 c数组的第u位数是否距离在2以内
    public static boolean check(int[] c,int i,int u){
        int d = Math.min(Math.abs(i - c[u]),n - Math.abs(i - c[u]));
        return d <= 2;
    }
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for(int i = 0;i < 3;i++){
            a[i] = sc.nextInt();
        }
        for(int i = 0;i < 3;i++){
            b[i] = sc.nextInt();
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= n;j++){
                for(int k = 1;k <= n;k++){
                    if(check(a,i,0) && check(a,j,1) && check(a,k,2) || 
                    check(b,i,0) && check(b,j,1) && check(b,k,2)){
                        cnt++;
                    }
                }
            }
        }
        System.out.println(cnt);
    }
}

7 评论

用户头像
花终会凋零   2022-04-18 20:05      1    踩      回复

当n > 5时, d <= 5 时, 两边都有可能出现公共部分，都需要判断

#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>

using namespace std;

int a[4], b[4];
int ans;

int main()
{
    int n;
    cin >> n;

    for (int i = 1; i <= 3; i ++ ) cin >> a[i];
    for (int i = 1; i <= 3; i ++ ) cin >> b[i];

    ans = 2 * min(n, 5) * min(n, 5) * min(n, 5);

    int res = 1;
    for (int i = 1; i <= 3; i ++ )
    {
        int d = min(abs(a[i] - b[i]), n - abs(a[i] - b[i]));

        if (n <= 5)
        {
            res *= n;
        }
        else
        {
            int k = max(0, 5 - abs(a[i] - b[i]));
            int m = max(0, 5 - n + abs(a[i] - b[i]));
            res *= max(k + m, 0);
        }
    }

    cout << ans - res << endl;

    return 0;
}
用户头像
Lg_970   2022-04-18 00:43      1    踩      回复

容斥原理题解，求公共部分的时候少考虑了情况，（枚举可得规律）还是不大靠谱的。可以直接用数组打标记求公共部分，这样会稳妥很多。错误数据可能是后来加的：n=6 密码1：111 密码2：444 结果：186。

用户头像
Lg_970   2022-04-18 20:22      1    踩      回复

经提示，C++代码现修改如下：

#include <bits/stdc++.h>
using namespace std;

int a[3],b[3],flag[110];

int main(){
    int n;
    cin >> n;
    int res1=min(n,5)*min(n,5)*min(n,5)*2;

    //以上计算了两次公共密码，所以需要计算两类表盘的公共密码种数，采用"容斥原理"减去公共密码种数

    for(int i=0;i<3;i++) cin >> a[i];
    for(int i=0;i<3;i++) cin >> b[i]; //读入数据

    int res2=1;

    for(int i=0;i<3;i++){ //查找三个对应位置上公共数据的个数，最后相乘即可求res2（公共密码种数）
        memset(flag,0,sizeof flag);

        for(int pos=a[i]-2;pos<=a[i]+2;pos++) flag[(pos%n+n)%n]++;

        int cnt=0;
        for(int pos=b[i]-2;pos<=b[i]+2;pos++) if(flag[(pos%n+n)%n]) cnt++;

        res2*=min(n,cnt);
    }
    cout << res1-res2;
    return 0;
}
用户头像
vanBo   6个月前         踩      回复

用st状态数组标记，求解每一位交集元素的个数即可

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int n;
int a[3], b[3];
int st[110];

int single()
{
    int res = 0;
    if (n <= 5)
        res = n * n * n;
    else 
        res = 5 * 5 * 5;
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < 3; i ++) scanf("%d", &a[i]);
    for (int i = 0; i < 3; i ++) scanf("%d", &b[i]);

    int both = 1;
    for (int i = 0; i < 3; i ++)
    {
        int cnt = 0;
        memset(st, 0, sizeof st);
        for (int j = a[i] - 2; j <= a[i] + 2; j ++)
        {
            int u = j - 1;
            u = (u + n) % n + 1;

            if (!st[u]) st[u] = 1;
        }

        for (int j = b[i] - 2; j <= b[i] + 2; j ++)
        {
            int u = j - 1;
            u = (u + n) % n + 1;

            if (st[u]) st[u] = 0, cnt ++;
        }
        both *= cnt;
    }

    int res = single() * 2 - both;
    printf("%d\n", res);
    return 0;
}
用户头像
XwX   2022-04-18 19:38         踩      回复

好像都有些问题。。

用户头像
无妍   2022-04-18 18:15         踩      回复 
//C++改，并修复漏洞
#include<iostream>
#include<cmath>
using namespace std;
int main(){
    int N=0;
    cin>>N;
    int ans=0;
    int n1[3],n2[3];
    for(int i=0;i<3;i++){
        cin>>n1[i];
    }
    for(int i=0;i<3;i++){
        cin>>n2[i];
    }
    if(N<=5){                           //N小于等于5时，二者范围必然完全相同，直接计数一者即可
        cout<<N*N*N;
        return 0;
    }
    int temp=1;
    int re=N-5;
    for(int i=0;i<3;i++){
        int n=min(abs(n1[i]-n2[i]),N-abs(n1[i]-n2[i]));
        if(re-n>=0)temp*=max(0,5-n);    //当N大于等于10时，只在两点在环上截取的劣弧能有重合
        else temp*=max(0,5-n)+n-re;     //当N大于5小于10时两点在环上截取的优弧也可能有重合
    }
    cout<<(250-temp);
}
用户头像
MOTSA   2022-01-06 09:59         踩      回复

感谢楼主分享，补充一下容斥原理c++的代码：

#include <bits/stdc++.h>

using namespace std;

int a[3], b[3];

int n;
int main () {
    cin >> n;
    for (int i = 0; i < 3; i++) {
        cin >> a[i];
    }

    for (int j = 0; j < 3; j++) {
        cin >> b[j];
    }

    int single = 2 * min(n, 5) * min(n, 5) * min(n, 5);
    int both = 1;
    for (int i = 0; i < 3; i++) {
        int d = min(abs(a[i] - b[i]), n - abs(a[i] - b[i]));
        if (n >= 5) {
            both *= max(0, 5 - d);
        } else {
            both *= n;
        }
    }
    cout << single - both << endl;
    return 0;
}