题目描述

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
如果图中存在负权回路，则输出“Yes”，否则输出“No”。

数据范围
1≤n≤2000,
1≤m≤10000,
图中涉及边长绝对值均不超过10000。

样例

输入样例：
3 3
1 2 -1
2 3 4
3 1 -4
输出样例：
Yes

拓展+题解 Acwing 361 观光奶牛

用spfa求负环的两个问题：
1.为什么一开始将所有点入队：
等价于加入一个虚拟源点，求从虚拟源点到每个点的最短路径，并且从虚拟源点到每个点的边权等于零，因此虚拟源点入队更新后会将所有点加入队列，等价于一开始就将所有点加入队列。

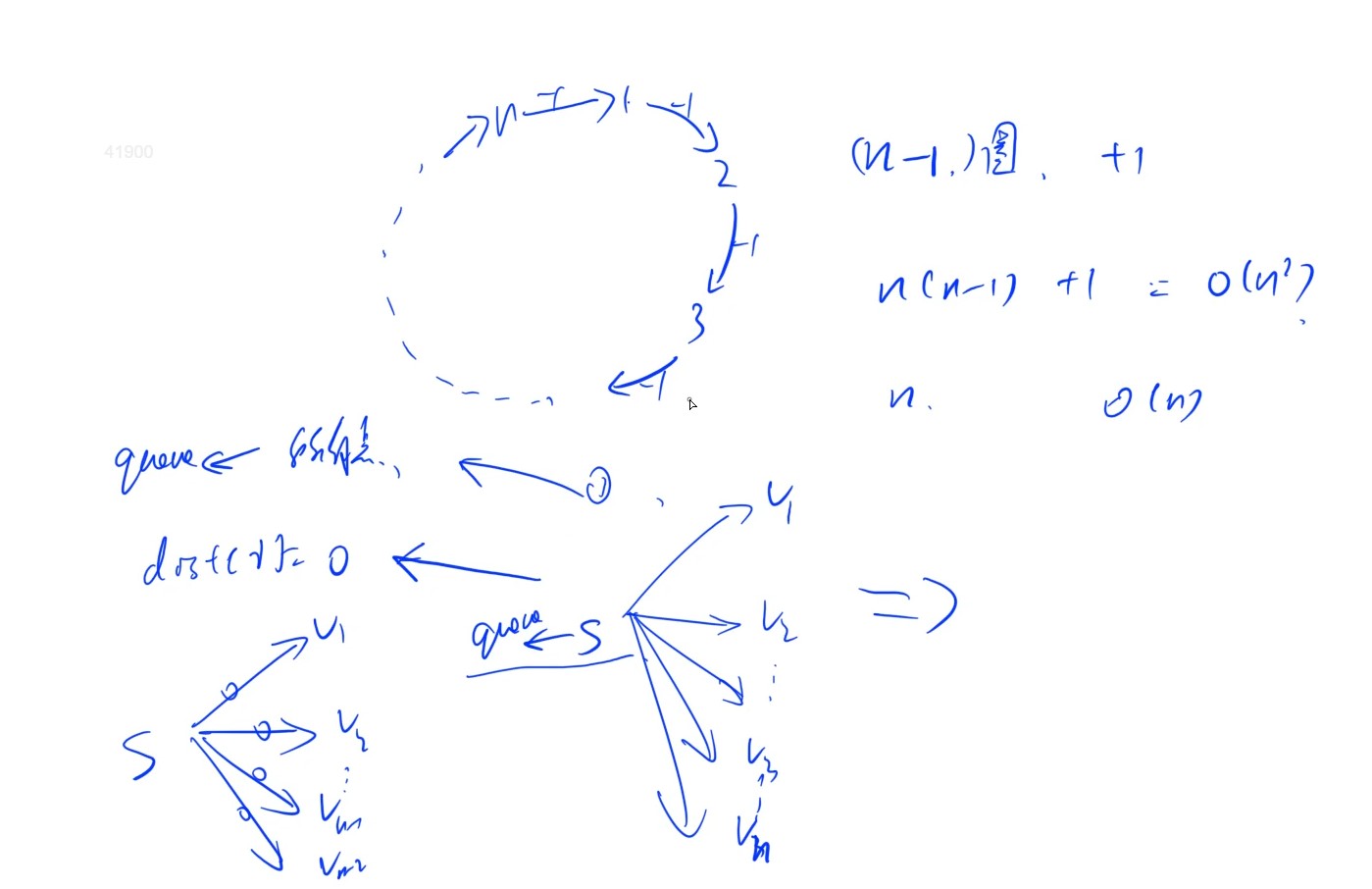
2.为什么dist不用初始化为正无穷或或零：
由于图中存在负环，并且是判断有没有负环，因此不需要用dist储存距离（求最短路径时要初始化为正无穷，因为要求最短路径，即最短距离），此处的dist只需要来判断是否比上一次距离小，是否需要更新，而当存在负环时，处在负环上的点是需要无限更新的，每绕一圈，路径就会减小，因此cnt是不断增大的，只需要根据cnt来判断是否存在负环即可

———————————————————

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

typedef pair<int ,int >PII;

const int N=1e5+10;

int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N],cnt[N];//cnt[x]表示以x为终点的最短路径的长度，
                               //cnt中若出现了以x为终点的最短路径长度>=n，则表示此路径有负环，即此图存在负环
                               //证明：
                               //cnt中若出现了以x为终点的最短路径长度>=n，则表示路径中有n+1个点
                               //，由抽屉原理可知路径中出现了环，而cnt[x]的更新是当dist[x]更新时随之更新，即dist变小时更新，因此
                              //此环必定是使得dist[x] 减小了,所以此环必定是负环，因此spfa可以用来找负环，由于找的是所有的负环，所以起点可以是虚拟源点
                              //此dist[x]存的是所有以x为终点的最短路径，一旦出现dist[x]某条路径中cnt[x]>=n，
                              //则表示图中有负环
bool st[N];

void add(int a,int b,int c){
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa(){//用spfa判断负环
    queue<int>q;
    memset(dist ,0x3f,sizeof dist);
    for(int i=1;i<=n;i++)//起点是n个点中的任何一个点，下面的spfa求的是以x为终点的所有最短路径
    {
        st[i]=true;//表示该点是否在队列中
        q.push(i);
    }
    while(q.size()){
         int x=q.front();
         q.pop();
         st[x]=false;
         for(int i=h[x];i!=-1;i=ne[i]){
             int j=e[i];
             if(dist[j]>dist[x]+w[i]){
                 dist[j]=dist[x]+w[i];
                 cnt[j]=cnt[x]+1;//由于dist可更新，则对应的
                                 //最短路径长度也可更新且为cnt[x]+1
                 if(cnt[j]>=n)return true;//当某次更新此点的某条最短路径时，路径长度大于等于n,
                                             //则证明此路径即此图存在负环
                 if(!st[j]){//只有当前的距离变小了，它的出边的距离才会变小，因此要加入队列，当此点未加入队列时，就加入队列
                            //，如已经加入则不用再加，重复加入没有意义
                     st[j]=true;
                     q.push(j);
                 }
             }
         }
     }

return false;
}
int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c); 
    }
  if(spfa())puts("Yes");
  else puts("No");
    return 0;
}