题目描述

In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.

(Note that backslash characters are escaped, so a \ is represented as "\\".)

Return the number of regions.

Example 1:

Input:
[
  " /",
  "/ "
]
Output: 2
Explanation: The 2x2 grid is as follows:

Note:

1. 1 <= grid.length == grid[0].length <= 30
2. grid[i][j] is either '/', '\', or ' '.

题意：在由 1 x 1 方格组成的 N x N 网格 grid 中，每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。返回区域的数目。

算法1

(并查集)

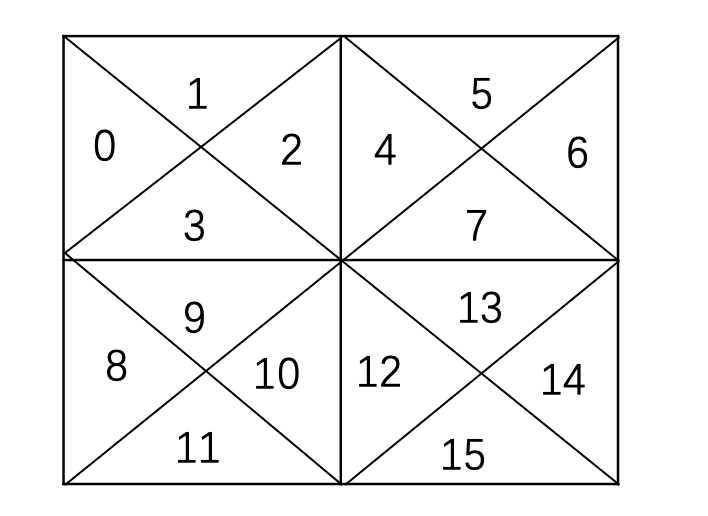
题解：这题如果了解并查集的话还是很好做的。首先我们将每个方格按照对角线划分成四个区域，如下图所示，并且从按照顺时针方向为其编号。初始时每一个格子内部右边和右边格子内部左边是连通的，如（2，4），没个格子的内部下边和下边格子的内部上边是连通的（3，9）。接下来，我们读取每一个格子的字符：

• /，那么把内部的左格子和上格子合并（0，1），右格子和下格子合并（2，3）。
• \，那么把内部的左格子和下格子合并（0，3），右格子和上格子合并（1，2）。
• ，那么把内部四个格子合并。

最后统计一下所有的连通块个数。

C++ 代码

class Solution {
public:
    vector<int> father,size;
    int getfather(int x)
    {
        if(x != father[x]) father[x] = getfather(father[x]);
        return father[x];
    }
    void uni(int x,int y)
    {
        int fatherA = getfather(x),fatherB = getfather(y);
        if(fatherA == fatherB) return;
        if(size[fatherA] < size[fatherB])
        {
            father[fatherA] = fatherB;
            size[fatherB] += size[fatherA];
        }
        else
        {
            father[fatherB] = fatherA;
            size[fatherA] += size[fatherB];     
        }
    }
    int regionsBySlashes(vector<string>& grid) {
        int n = grid.size(),m = 4 * n * n;
        father = vector<int>(m,0),size = vector<int>(m,1);
        for(int i = 0 ; i < m; i ++) father[i] = i;
        for(int i = 0 ;i < n ;i ++)
        {
            for(int j = 0 ;j < n ; j ++)
            {
                int k = i * n + j,t = (i + 1) * n + j,s = k + 1;
                if(i != n - 1) uni(4 * k + 3,4 * t + 1);
                if(j != n - 1) uni(4 * k + 2,4 * s);
            }
        }
        for(int i = 0 ;i < n ; i ++)
        {
            for(int j = 0 ;j < n ; j ++)
            {
                int k = 4 * (i * n + j);
                if(grid[i][j] == '/')
                {
                    uni(k,k + 1);
                    uni(k + 2,k + 3);
                }else if(grid[i][j] == ' ')
                {
                    uni(k,k + 1);
                    uni(k + 2,k + 3);
                    uni(k + 1,k + 2);
                }
                else
                {
                    uni(k,k + 3);
                    uni(k + 1,k + 2);
                }
            }
        }
        int res = 0;
        for(int i = 0 ;i < m ;i ++)
            if(i == getfather(i))
                res ++;
        return res;
    }
};