肖然博客

问题等价

说明：对于此题可以首先考虑让$B$变成非降序列的最小代价，而非增序列只需要reverse一下取最优即可，下面对本题只考虑变成非降序列的最小代价

首先我们先考虑下面的问题 CF13C Sequence

给定一个序列$A$，每次操作可以把某个数 $+1$ 或 $-1$。询问把原序列变成非降数列$B$的最小操作次数。

首先不难看出此题和上面的题目对每个数变得的代价计算是相同的：$|B_i-A_i|$，而且都所求也相同，可以说两个问题的本质是相同的。

而对于上面的题目如果$0\leq A_i\leq n$，则有一个显然的dp：

状态表示：$f_{i,j}$考虑前$i$个数，且第$i$个数的值是$j$即最终$B_i=j$的最优解
状态转移：$f_{i,j}=\min(f_{i-1,k}+|A_i-j|,k\leq j)=\min(f_{i-1,k})+|A_i-j|,k\leq j$
枚举$k$转移是$O(n)$的，不过如果记录前缀最小值即$\min(f_{i-1,k})$只需要$O(1)$转移，最终时间复杂度$O(n^2)$

再给力一些?

首先如果将上面的dp数组对于每个$i$看出$j$的函数即$y=f_{i,j}(j)$，打表可以发现这个函数是凹的

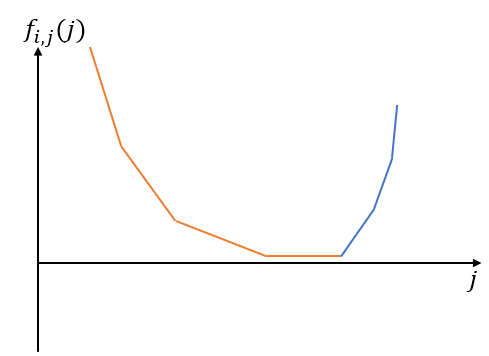
其实不用打表，原因和很简单绝对值函数相加最终函数一定是凹的即$$f(x)=|x-a_1|+|x-a_2|+\dots +|x-a_k|$$
$f(x)$一定是凹函数，而上面转移过程都是这些函数相加的过程，因此$y=f_{i,j}(j)$是凹函数。

考虑$i$而对于每一个$f_{i,j}(j)$我们想要快速求得它的拐点位置（下面也叫其决策点$opt_i$）因为拐点位置对应的$f_{i,j}(j)$值最小，也就是最优解。

当$dp$到第$i$行我们试图快速求出

我们尝试维护上图中橘黄色的一些线段的斜率的绝对值。

• $opt_i$
• 维护$f_{i,j}(j)$

如果$a_i\ge opt_{i-1}$：

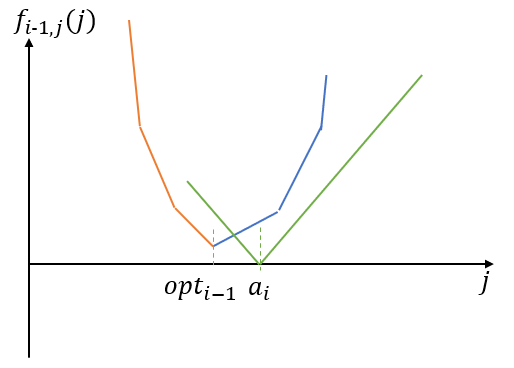
不难发现两函数叠加后拐点是$a_i$也就是$opt_i=a_i$且小于$a_i$位置斜率绝对值+1
且$f_{i}(opt_i)=f_{i-1}(opt_{i-1})$

如果$a_i<opt_{i-1}$：

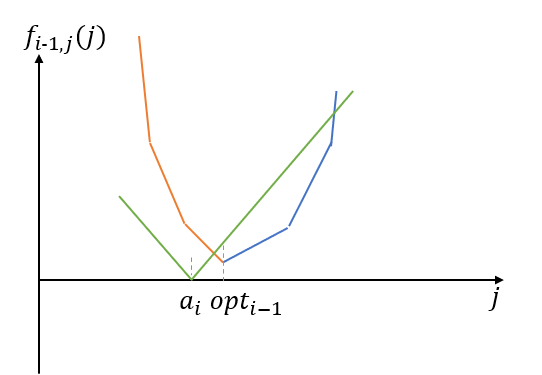
而此时函数大于$a_i$位置部分橘色部分线段斜率绝对值-1，而小于$a_i$位置橘色部分线段斜率绝对值+1

且由图像可知$f_{i}(opt_i)=f_{i-1}(opt_i)+opt_i-a_i$

对于上述情况，拐点始终是斜率为0时刻最右边的端点。

对于维护斜率，使用优先队列存储（橘色）每一段的右端点，并定义：

斜率rank(i) = 队列中>=i的数的个数

第一种情况：小于$a_i$斜率绝对值+1，只需要将$a_i$插入即可
第二中情况：大于$a_i$位置部分橘色部分线段斜率绝对值-1，而小于$a_i$位置橘色部分线段斜率绝对值+1，只需要插入两次$a_i$并且将对头pop即可。

优先队列的对头始终都是维护的决策点。

详细见代码$O(n\log n)$

而对于本题非增或非减只需要reverse一下即可。

#include<queue>
#include<iostream>
#include<algorithm>
using namespace std;
using ll=long long;
constexpr int N=500010;
int n,a[N];

ll work()
{
    ll ans=0;
    priority_queue<int> q;
    for(int i=1;i<=n;i++)
    {
        q.push(a[i]);
        if(a[i]<q.top()) 
        {
            ans+=q.top()-a[i];  //代价
            q.push(a[i]);q.pop();
        }
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);

    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    ll ans=work();
    reverse(a+1,a+1+n);
    ans=min(ans,work());
    cout<<ans<<'\n';

    return 0;
}