算法思想

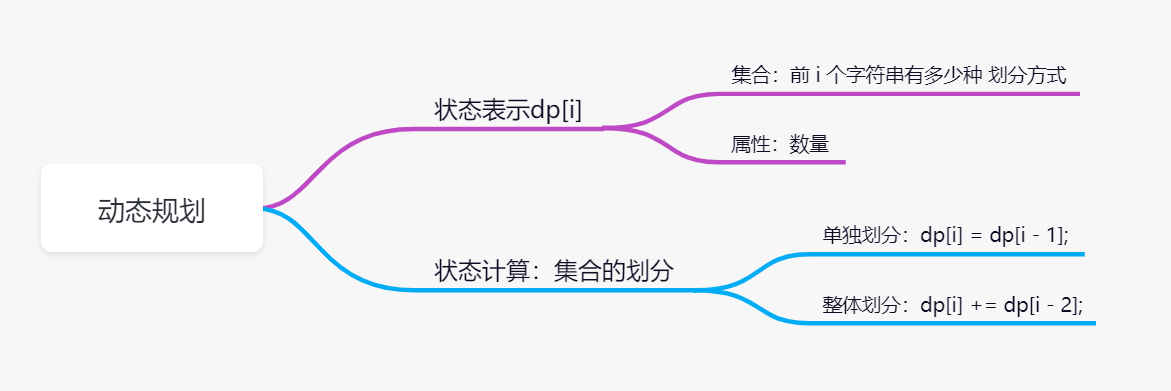
一般计数的问题 要用dp来做，至于什么时候可以用dp，这个一般是以前自己遇到过相似的模型，然后可以想到并且确认用dp；

集合的属性是最容易得出来得，问题问的什么属性就是什么，即属性

集合的表示是参考 以前遇到的模型，前i个字符有多少种划分方式，

集合的划分是按照翻译的方式进行划分，分为两种，单独翻译和整体翻译，状态划分方程我是模拟例子得出来得；

举例：1 2 8

dp[0] = 0; 字符：

dp[1] = 1; 字符：1

dp[2] = 2; 字符：1 2 划分方式：1,2 12

dp[3] = 2; 字符：1 2 8 划分方式：1,2,8 12, 8

我们可以发现如果是单独划分，那么前i个字符是和前i - 1相等的; 参考增加8

但是如果可以整体划分，那么还得加上前i-2个字符的划分数，因为前i-2的划分可以和目前的整体划分组合起来，有新的划分方式出现。参考增加2

问题

问题1：为什么是s.charAt(i - 2) 和 s.charAt(i - 1)

因为dp[i] 表示的是前 i 个字符，但是我们的字符串是从0开始计数的，当前字符的索引是i - 1，前一个字符的索引是i - 2：

举例：128，前2个字符表示的是12，那么第i个字符的索引是 i-1，前一个字符的索引是i - 2；

问题2：为什么f[0] = 1

我们知道f[1]表示前1位数只有一种翻译方式，单独翻译，所以为1
在计算f[2]的时候，f[2] = f[1] = 1,如果可以组合翻译的话，答案应该是2, f[2] = f[2] + f[0] = 2 ==>f[0] = 1;

问题3：为什么是>= 10,而不是0

因为01是无法组合翻译的，只能单独翻译，而10以后可以；

java代码

class Solution {
    public int getTranslationCount(String s) {
        int n =  s.length();
        int[] f = new int[n + 10];            //前i位数字有多少种翻译方式
        f[0] = 1;
        f[1] = 1;
        for(int i = 2; i <= n; i ++)
        {
            f[i] = f[i - 1];                 //第i位单独翻译
            int t = (s.charAt(i - 2) - '0') * 10 + s.charAt(i - 1) - '0';
            if(t >= 10 && t <= 25) f[i] += f[i - 2];   //组合翻译
        }

        return f[n];
    }
}