题目描述

给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。

对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。

如果数组中不存在该元素，则返回“-1 -1”。

输入格式
第一行包含整数n和q，表示数组长度和询问个数。

第二行包含n个整数（均在1~10000范围内），表示完整数组。

接下来q行，每行包含一个整数k，表示一个询问元素。

输出格式
共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回“-1 -1”。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000

样例

输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

算法1

二分法

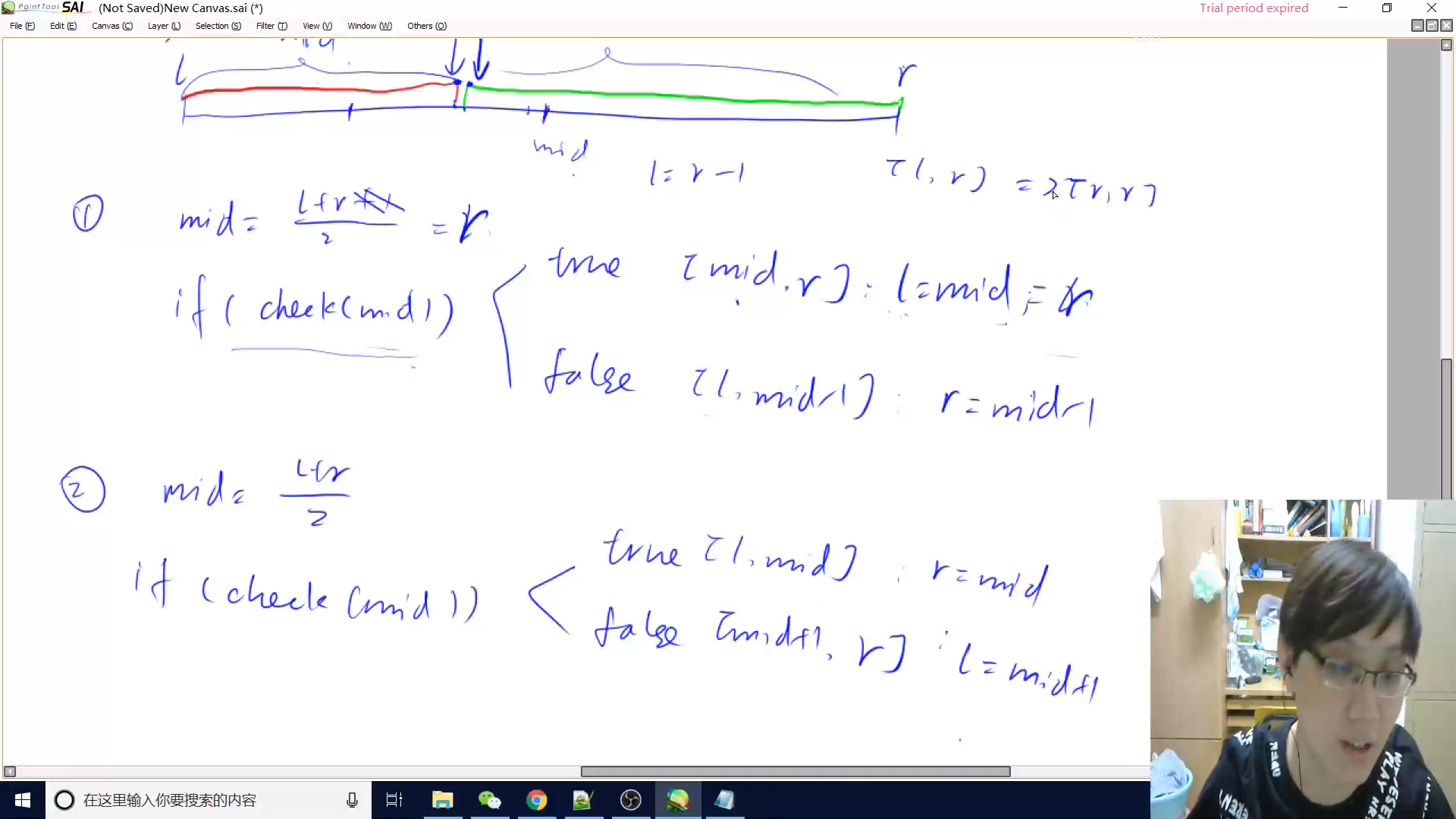
时间复杂度

log(n)

python 代码

if __name__ == "__main__":
    n,m = map(int,input().split())
    q = list(map(int,input().split()))
    for i in range(m):
        x = int(input())
        l=0
        r=n-1
        while l<r:
            mid = (l+r)//2
            if q[mid]>=x:       #性质定义为>=x,右边都满足，因此可以找到左边界
                r=mid           #mid满足性质，更新时要包含mid
            else:
                l=mid+1
        if q[l] != x:
            print("-1 -1")
        else:
            print(l,end=" ")
            l=0
            r=n-1
            while l<r:
                mid = (l+r+1)//2
                if q[mid]<=x:   #性质定义为<=x,左边都满足，右边都不满足，因此可以找到右边界
                    l=mid      #l=mid时，上面求mid要+1。
                else:
                    r=mid-1     #mid不满足性质，答案在l到mid-1之间，所以至少要从mid-1开始
            print(l)