@TOC

剑指 Offer 03. 数组中重复的数字

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出： 2 或 3

限制：
$2 <= n <= 100000$

解法一：建立一个新数组打卡标记

1. 所有数字都在0 ~ n - 1之间，所以可以建立一个长度为n的数组辅助数组temp，将原数组中元素的数值作为temp数组的下标索引值进行计数，用来记录每个数字出现了多少次。
2. 遍历数组temp,当前元素大于1的话，说明出现次数大于1，即重复了，返回该元素的索引即可，因为索引对应的就是原数组中的元素值。

时间复杂度： 遍历数组 $O(n)$
空间复杂度： 开辟了大小为n的辅助数组 $O(n)$

class Solution {
    public int findRepeatNumber(int[] nums) {
        //检查参数合法性
        if(nums == null || nums.length == 0) return -1;
         //数组中有数字不在0~n-1范围内时不符合题意，直接返回-1
        for(int i = 0;i < nums.length;i++){
            if(nums[i] < 0 || nums[i]>nums.length-1) return -1;
        }
        int[] temp = new int[nums.length];//声明数组用于标记nums数组中每个数字出现的次数
        for(int i = 0; i < nums.length; i++){
            temp[nums[i]]++;
        }
        for(int i = 0; i < temp.length; i++){
            if(temp[i] > 1){//次数大于1，i就是重复的
                return i;//注意返回的是i，temp[i]是出现的次数，i才是重复的数字
            }
        }
        return -1;//没有重复的数字
    }
}

解法二：移动元素让下标和值相对应

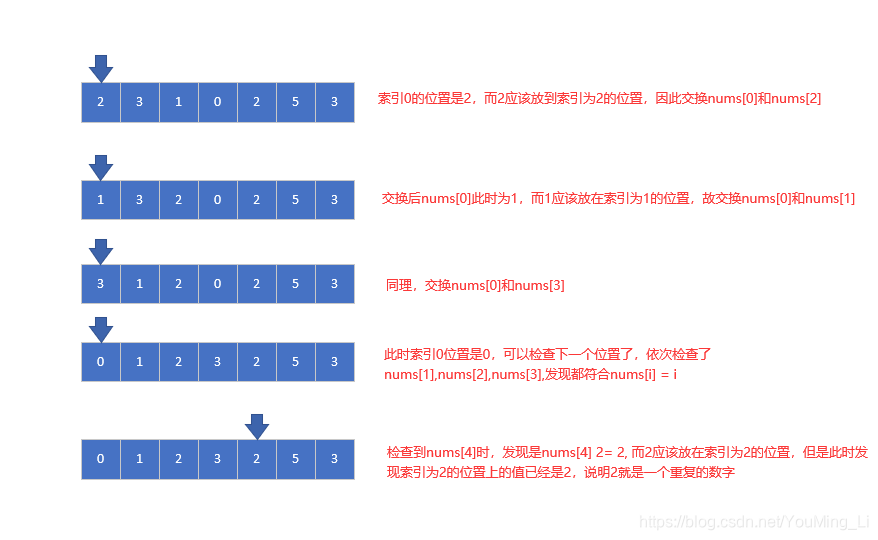
将每个元素放到与下标对应的地方，如2应该放在nums[2]的位置，如果下标0的位置是2，则不满足nums[0] = 0，而是应该将下标0处的元素2放到nums[2]的位置，而如果经过比较发现nums[2]的位置本身就是2了，说明2就是重复的数字。详细过程如下图：

时间复杂度： 遍历数组 $O(n)$
空间复杂度： 并未开辟额外空间 $O(1)$

class Solution {
    public int findRepeatNumber(int[] nums) {
        //检查参数的合法性
        if(nums == null || nums.length == 0) return -1;

        for(int i = 0; i < nums.length; i++){
            while(nums[i] != i){ //注意这里是while，而不是if,因为换回来的数字，也要放到正确的位置去
                if(nums[i] == nums[nums[i]]){//nums[i]应该放到下标为nums[i]的位置的
                    return nums[i];
                }
                //不相等，则交换，将nums[i]放到与下标对应的位置去
                int temp = nums[nums[i]];
                nums[nums[i]] = nums[i];
                nums[i] = temp;
            }
        }
        return -1;
    }
}

解法三：将数组排序，判断相邻两个数是否相等

时间复杂度： 用到快速排序 $O(nlogn)$

class Solution {
    public int findRepeatNumber(int[] nums) {
        //检查参数合法性
        if(nums == null || nums.length == 0) return -1;
        Arrays.sort(nums);//将数组排序，默认快排
        for(int i = 0; i < nums.length; i++){
            if(i !=0 && nums[i] == nums[i-1] ){//当前数字和前一个数字相同
                return nums[i];
            }
        }
        return -1;
    }
}

解法四：利用HashSet记录，出现重复数字时立马返回结果即可

class Solution {
    public int findRepeatNumber(int[] nums) {
        //检查参数合法性
        if(nums == null || nums.length == 0) return -1;
         Set<Integer> set = new HashSet<>();
         for(int i = 0; i < nums.length;i++){
             if(set.contains(nums[i])){
                 return nums[i]; //该数字已经存在于set中，重复了
             }else{
                 set.add(nums[i]);//该数字不在set中，添加进去
             }
         }
         return -1;
    }
}

第三题的扩展题：不修改数组找出重复的数字 LeetCode 287

287. 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，找出 这个重复的数 。

示例 1：

输入： nums = [1,3,4,2,2]
输出： 2

示例 2：

输入： nums = [3,1,3,4,2]
输出： 3

示例 3：

输入： nums = [1,1]
输出： 1

示例 4：

输入： nums = [1,1,2]
输出： 1

提示：

• $2 <= n <= 3 * 10^4$
• $nums.length == n + 1$
• $1 <= nums[i] <= n$
• $nums$ 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

进阶：

如何证明 $nums$ 中至少存在一个重复的数字?
你可以在不修改数组 $nums$ 的情况下解决这个问题吗？
你可以只用常量级 $O(1)$ 的额外空间解决这个问题吗？
你可以设计一个时间复杂度小于 $O(n^2)$ 的解决方案吗？

思路

1. 不能修改原数组，故不能用移动元素让下标和值相对应的方法，也不能用排序的方法
2. 只能用$O(1)$的空间，故不能用HashSet和新数组打卡标记的方法
3. 时间复杂度小于$O(n^2)$,故不能用暴力嵌套两个for循环遍历数组两次的方法

### 使用分治法

​ 注意：分的区间是数的范围，而不是索引的范围，如果在这个数字区间的数字个数大于索引区间长度，那么这个区间内一定有数字重复了，继续对该区间进行划分，直到区间长度为1为止。

如：数组[2,3,3,2,5,4,6,7],这个长度为8的数组的所有元素都在1 ~ 7范围内，中间的数字4（注意不是索引4）把数字1 ~ 7范围分为了两段，一段是1 ~ 4，一段是5 ~ 7，接着统计1 ~ 4这4-1+1=4个数字在整个数组中出现的次数，发现是5次，因此重复的数字一定是在1 ~ 4中的。

​ 时间复杂度： 分治法为$O(logn)$，每次都要统计区间范围内的数字，复杂度为$O(n)$,所以总的复杂度为$O(nlogn)$。

class Solution {
    public int findDuplicate(int[] nums) {
        //检查参数的合法性
        if(nums == null || nums.length == 0) return -1;
        //数组中的数字在1~n之间，故按数字的范围二分，left和right起始值如下
        int left = 1;//数字最小为1
        int right = nums.length - 1;//由题意知，nums.length = n + 1，故n=nums.length-1
        while(left < right){//当left=right时，即只剩下一个数时停止循环，那个数就是结果
            int mid = (left + right)/2;
             //计算整个数组在前半部分的个数
            int count = getCount(nums,left,mid);
            if(count > (mid - left +1)){//个数大于区间本该有的个数，该区间出现了重复数字
                right = mid;
            }else{
                left = mid+1;//注意是mid+1,不是mid
            }
        }
        return left;//实际上最后返回left还是right都可以，因为他们最后相等
    }

    public int getCount(int[] nums,int left,int right){
        int count = 0;
        for(int num : nums){
            if(num >= left && num <= right){//统计left~right（假设是1~4）这right-left+1（=4）个数字在整个数组中出现的次数
                count++;
            }
        }
        return count;
    }
}