剑指offer 10-I 斐波那契数列 LeetCode509
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: n = 2
输出: 1
示例 2:
输入: n = 5
输出: 5
提示:
0 <= n <= 100
面试小提示
基于递归实现代码比基于循环实现代码要简洁很多,也更加容易实现,如果面试官没有特殊要求,则可以用递归的方法编程。但递归虽然简洁,却也有一些缺点:
1. 递归就是函数调用自身,而函数调用是有时间和空间消耗的
2. 递归层数太深的话,会导致栈溢出。
3. 递归中间可能有很多重复的计算。
采用递归的方式实现斐波那契数列弊端
class Solution {
public int fib(int n) {
if(n<=0) return 0;
if(n == 1) return 1;
return fib(n-1) + fib(n-2);
}
}
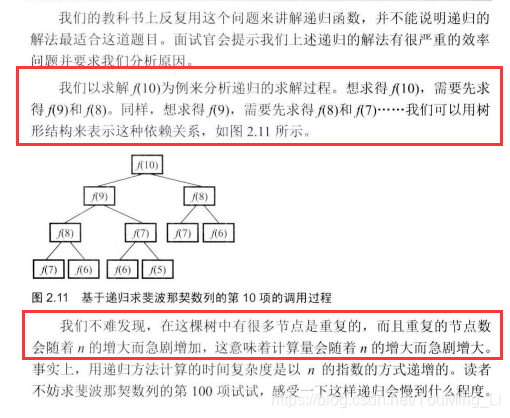
上图是《剑指offer》第二版75页原图。
用循环的方式能够避免重复的计算
class Solution {
public int fib(int n) {
int a = 0;
int b = 1;
int c = 0;
while(n-- > 0){
c = (a+b) % 1000000007;
a = b;
b = c;
}
return a;
}
}
剑指offer 10-II 青蛙跳台阶问题 LeetCode70
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: n = 2
输出: 2
示例 2:
输入: n = 7
输出: 21
示例 3:
输入: n = 0
输出: 1
提示:
0 <= n <= 100
注意:本题与主站 70 题相同:https://leetcode-cn.com/problems/climbing-stairs/
解法一:递归方式
虽然本题没有明说是斐波那契数列,但经过分析会发现其实就是斐波那契数列的应用。思路和斐波那契数列的递归完全一样,我将在本处引出很多其他应用。
公式这里显示不出来,请看本人博客 10.2 青蛙跳台阶问题与矩形覆盖问题
思路:用递归的方法,例如,第一次跳有两种不同的选择
[HTML_REMOVED][HTML_REMOVED][HTML_REMOVED]1. 爬一个台阶,则此时爬法数目等于后面剩下n-1阶的爬法数目climbStairs(n-1)
[HTML_REMOVED][HTML_REMOVED][HTML_REMOVED]2. 爬两个台阶,则此时爬法数目等于后面剩下n-2阶的爬法数目climbStairs(n-1)
[HTML_REMOVED][HTML_REMOVED]总的爬法数目climbStairs(n) = climbStairs(n-1)+climbStairs(n-2)
由上可知,这是斐波那契数列问题,该处用递归的话,有很多计算是重复的,耗时长
注:本题递归的方式提交的时候会超时,另外代码中用到了(a + b) % p = (a % p + b % p) % p。
递归代码
class Solution {
public int climbStairs(int n) {
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
int num1 = climbStairs(n-1) % 1000000007;
int num2 = climbStairs(n-2) % 1000000007;
return (num1 + num2) % 1000000007;
}
}
解法二:循环方式
由于递归存在重复计算的问题,故我们考虑改用循环的方法,只是本题起点是1,2(第一步跳一个台阶或者两个台阶),而不是传统的0,1。
class Solution {
public int numWays(int n) {
int a = 1;
int b = 2;
int c = 0;
//注意此处是n-1,而不是n,因为前两个数a,b已经直接给出了,现在只要计算到n-2即可
for(int i = 0;i < n-1;i++){
c = (a + b) % 1000000007;
a = b;
b = c;
}
return a ;
}
}

解法三:动态规划
青蛙跳台阶其实也是一个典型的动态规划的例题,用dp[i]表示跳到第i个台阶的跳法
状态转移:dp[i] = dp[i-1]+dp[i-2]
class Solution {
public int numWays(int n) {
//由于dp[n]表示的是跳到第n个台阶的跳法,所以数组长度应该是dp[n+1]
//如果数组长度是n,则dp[n]将出现数组下标越界问题
int[] dp = new int[n+1];
if(n==0 || n == 1) return 1;
if(n == 2) return 2;
dp[1]=1;
dp[2]=2;
for(int i = 3;i <= n;i++){
dp[i] = (dp[i-1] + dp[i-2]) % 1000000007;
}
return dp[n];
}
}

青蛙变态台阶与矩形覆盖(剑指offer第十题后面的扩展题)
青蛙变态跳台阶
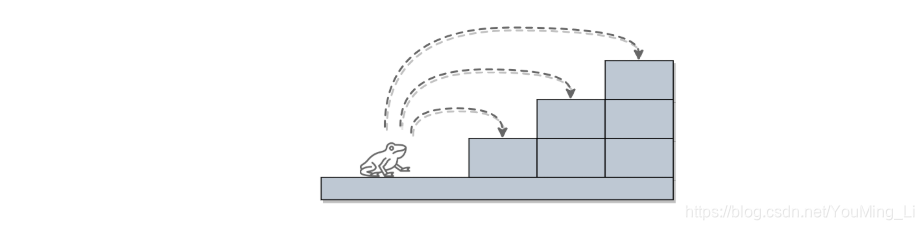
一直青蛙一次可以跳上 1 级台阶,也可以跳上 2 级…它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
解题思路
与之前可以跳上一级台阶或者两阶台阶类似,不过是可以跳上任意阶台阶而已,思路仍然是用动态规划,用dp[i]表示跳上第i阶台阶的跳法种数。则dp[i]=dp[i-1]+dp[i-2]+···+dp[0]
Java代码
class Solution {
public int numWays(int n) {
//由于dp[n]表示的是跳到第n个台阶的跳法,所以数组长度应该是dp[n+1]
//如果数组长度是n,则dp[n]将出现数组下标越界问题
int[] dp = new int[n+1];
if(n==0 || n == 1) return 1;
if(n == 2) return 2;
dp[1]=1;
dp[2]=2;
for(int i = 3;i <= n;i++){
for(int j = 0;j < i;j++ ){//dp[i]=dp[i-1]+dp[i-2]+···+dp[0]
dp[i] += dp[j];
}
}
return dp[n];
}
}
矩形覆盖
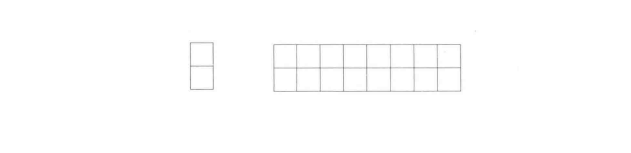
我们可以用 2×1 的小矩形横着或者竖着去覆盖更大的矩形。请问 n 个 2×1 的小矩形无重叠地覆盖 2×n 的大矩形,总共有多少种方法?
解题思路
要覆盖 2×n 的大矩形,有两种选择:竖着放或者横着放。
1. 当竖着放的时候,如下图所示,即先覆盖 2×1 的矩形,再覆盖 2×(n-1) 的矩形。

2. 当横着放的时候,如下图所示,当2×1的小矩形横着放在左上角的时候,左下角必须横着放一个2×1的小矩形,再覆盖剩下的 2×(n-2) 的矩形。

3. 覆盖 2×(n-1) 和 2×(n-2) 的矩形可以看成子问题。
从而得出该问题的递推公式:
$$ f(x)=\left\{
\begin{aligned}
1 &&&& n=1\\
2 &&&& n =2 \\
f(n-1)+f(n-2) &&&& n > 2
\end{aligned}
\right.
$$
Java代码
斐波那契循环写法
public int RectCover(int n) {
if (n <= 2)
return n;
int a = 1, b = 2;
int result = 0;
for (int i = 3; i <= n; i++) {
result = a + b;
a = b;
b = result;
}
return result;
}
动态规划写法
dp[i]表示用 2×1 的小矩形覆盖2*i的大矩形共有多少种方法,则dp[n]表示的便是用 2×1 的小矩形覆盖2*n的大矩形共有多少种方法。
状态转移:dp[i] = dp[i - 1] + dp[i - 2]
public int RectCover(int n) {
int[] dp = new int[n+1];
//初始化dp
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i = 3;i <= n;i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n]
}

