题目描述：

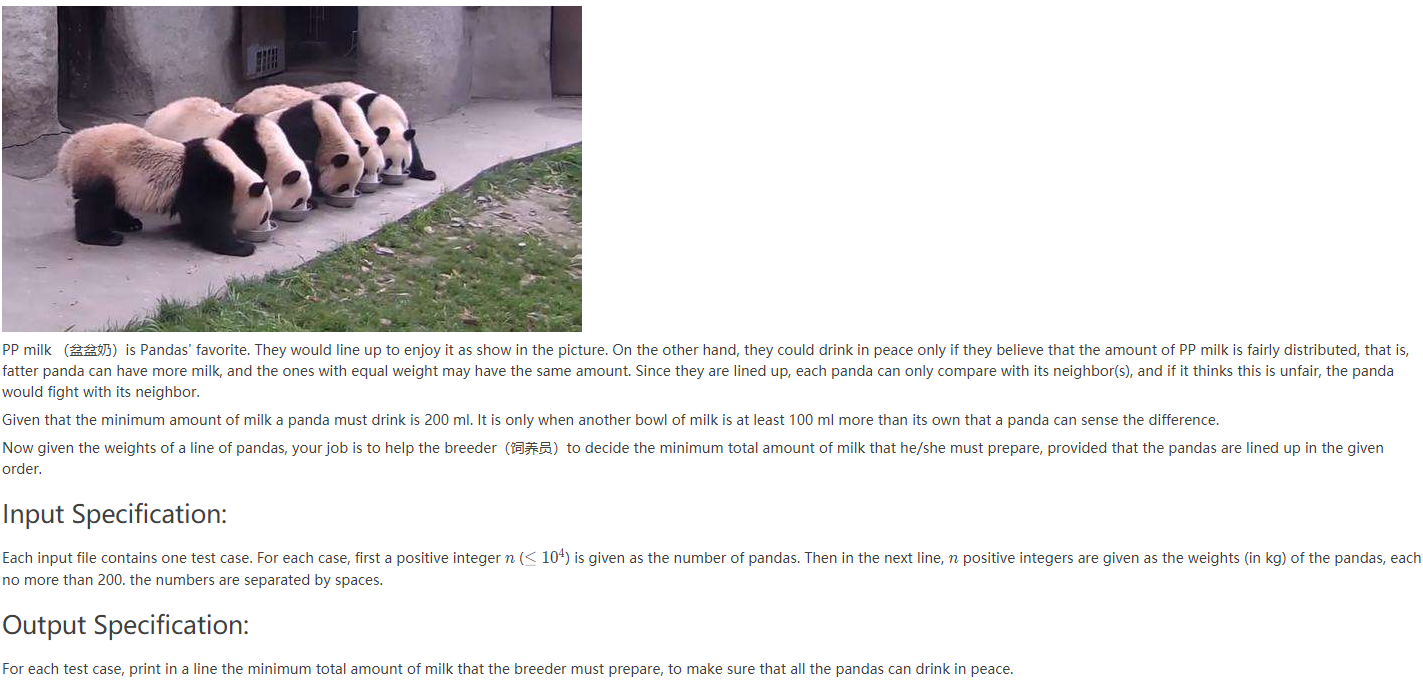
样例：

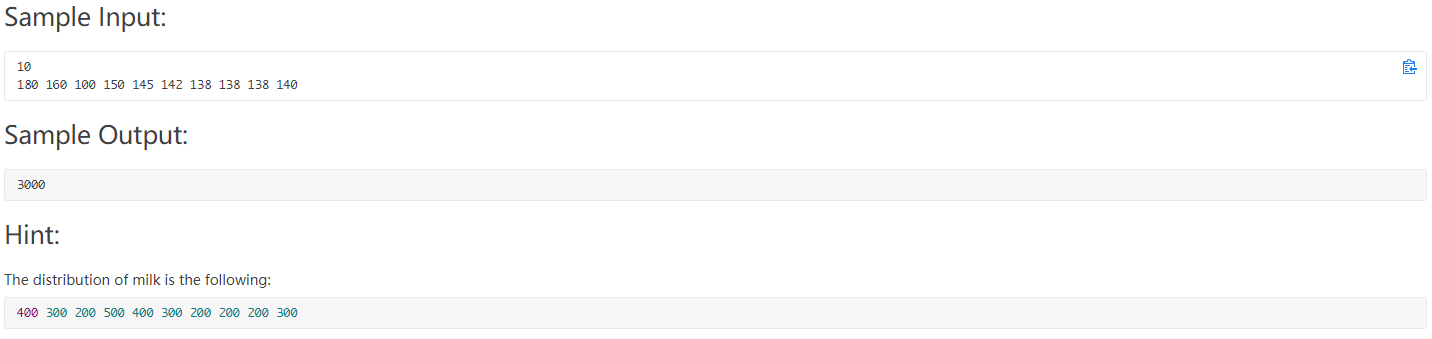
算法思路：

1、最初看到这道题的蒟蒻的第一个思路就是差分约束，不过本蒟蒻也知道放在第一个题肯定不需要上来就搞个图论，但是实在想不出其他更好的方法了，只能上来硬干了（貌似全网题解中也只有我杀鸡用牛刀用了差分约束呜呜）。

2、首先这题求的是最小值，那么差分约束就是求最长路，最长路可能涉及正环图而导致无解，但因为本题保证了一定有解，所以省去了cnt[i]判断正环的过程。

3、构造：用v[i]代表熊猫i的体重，w[i]代表熊猫i的奶量，那么如果v[i] > v[j], 则w[i] >= v[j] + 100，那么就要构造一个有j指向i的、边长为100的边；相等、小于的情况具体表示见下面的代码，因为题目要求每一个熊猫都要有至少200ml的奶量，即w[i] >= 200，因此可以构造0号虚拟源点，让w[i] >= w[0] + 200，即虚拟源点与每一个点都有一个长度为200的边，从而保证了源点到每个边的连通性，证明了算法正确。

C++ 代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;

const int N = 10010, M = 5 * N;
int v[N];                           // 熊猫体重
int h[N], e[M], w[M], ne[M], idx;   // 建图
int dist[N];                        // 最长路
int st[N];
int n;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// spfa求最长路
void spfa()
{
    memset(dist, -0x3f, sizeof dist);
    dist[0] = 0;
    stack<int> q;    // 使用栈优化spfa
    q.push(0);
    st[0] = true;

    while (!q.empty())
    {
        int t = q.top();
        q.pop();
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];

            if (dist[j] < dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++) scanf("%d", &v[i]);        // 录入每一个熊猫的体重

    // 建立l, i, r之间的不等关系
    for (int i = 1; i <= n; i++)
    {
        int l = i - 1, r = i + 1;                           // 跟左右两个熊猫比较
        if (l >= 1)
        {
            if (v[i] < v[l]) add(i, l, 100);
            else if (v[i] == v[l]) add(l, i, 0), add(i, l, 0);
            else add(l, i, 100);
        }
        if (r <= n)
        {
            if (v[i] < v[r]) add(i, r, 100);
            else if (v[i] == v[r]) add(r, i, 0), add(i, r, 0);
            else add(r, i, 100);
        }
    }

    // 建立虚拟源点, 保证每个熊猫有>=200ml牛奶
    for (int i = 1; i <= n; i++) add(0, i, 200);

    // 因为原题保证有解, 所以不需要判断正环
    spfa();

    int milk = 0;
    for (int i = 1; i <= n; i++) milk += dist[i];
    printf("%d\n", milk);

    return 0;
}