特殊计数序列——Catalan数

定理 考虑由 $n$ 个 $+1$ 和 $n$ 个 $-1$ 组成的 $2n$ 项序列
$$ a_1, a_2, \cdots , a_{2n} $$
其部分和总是满足
$$ a_1+a_2+\cdots + a_k \geqslant 0 \quad (\forall k = \{1, 2, \cdots, 2n \}) $$
这种序列的个数等于第 $n$ 个 Catalan 数
$$ C_n = \frac{1}{n+1} {2n \choose n} (n \geqslant 0) $$
证明如下

通过以上证明了任意不可接受序列 $U(n, n)$ 与序列 $C(n+1, n-1)$ 存在对应关系
$C(n+1, n-1)$ 的个数实际上就是排列数
$$ \frac{(2n)!}{(n+1)!(n-1)!} $$
从而
$$ U(n) = \frac{(2n)!}{(n+1)!(n-1)!} $$
$$ A(n) = {2n \choose n} - U(n) = \frac{1}{n+1}{2n \choose n} $$

计数类问题编程实现常用函数

阶乘分解

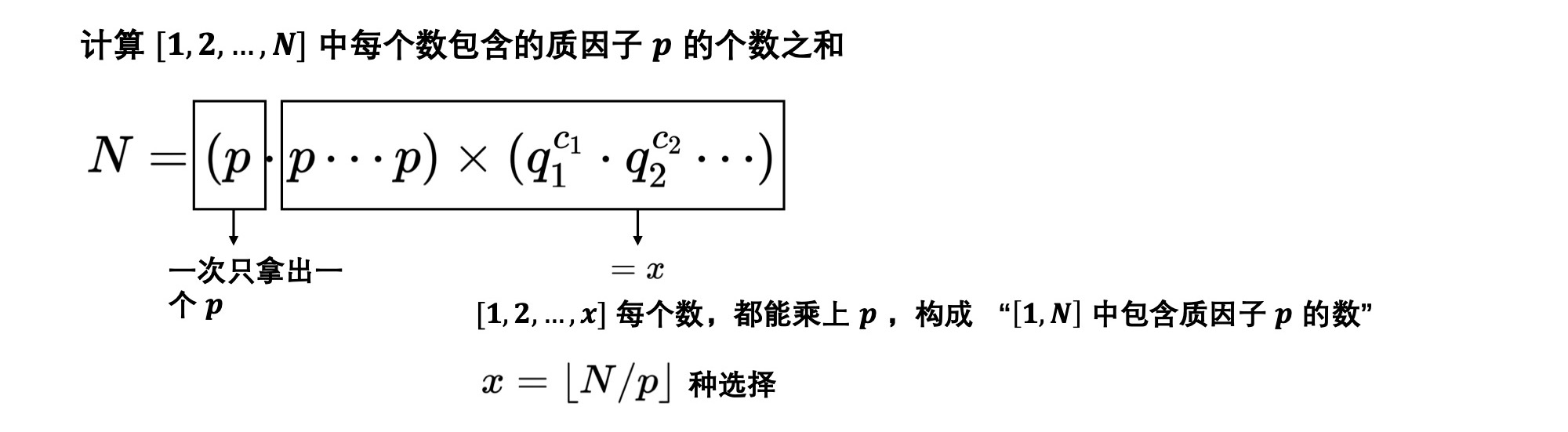
对于 $N!$ 进行阶乘分解的结果是
$$ \sum_{p^k \leqslant N} \lfloor \frac{N}{p_k} \rfloor $$

试除法分解质因数

void divide(int x) {
    for (int i = 2; i <= x/i; i++) {
        if (x % i == 0) {
            int s = 0;
            while (x % i == 0) s++, x /= i;
            // i^s
            make_pair(i, s);
        }
    }
    if (x > 1) make_pair(x, 1);
    // x^1
}

朴素筛法求质数

vector<int> primes;
bool st[maxn]; // init st[...] = 0
// st = true 表示这个数是合数

void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (st[i]) continue;
        primes.push_back(i);
        for (int j = 2*i; j <= n; j += i) st[j] = true;
    }
}

线性筛法求质数

vector<int> primes;
bool st[maxn];

void get_primes() {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes.push_back(i);
        for (int j = 0; primes[j] <= n/i; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j]) break;
        }
    }
}

Catalan 数经典应用

这里涉及到一个编程技巧，叫高精度压位
Acwing130

其实就是计算 Catalan 数
$$ \frac{1}{n+1} {2n \choose n} $$

• 打表 $[2, 2n]$ 所有的素数
• 阶乘分解，$\textbf{for} \ \forall p \in \textbf{primes}[\cdots]$
  求出 $\textbf{pw}[p]= \textbf{get}(2n, p) - 2\cdot \textbf{get}(n, p)$
  即素数 $p$ 在$2n \choose n$ 这项中的幂指
• 对 $n+1$ 进行素因子分解，$n+1 = \cdots p^s \cdots$，然后 $\textbf{pw}[p] -= s$
• $\textbf{for} \ \forall p \in \textbf{primes}[\cdots]:$ 执行 $\textbf{pw}[p]$ 次 $\textbf{muti}(ans, p)$

const int maxn = 120000 + 10;
int n;

vector<int> primes;
bool st[maxn];

void get_primes() {
    memset(st, 0, sizeof st);
    for (int i = 2; i <= 2*n; i++) {
        if (st[i]) continue;
        primes.push_back(i);
        for (int j = 2*i; j <= 2*n; j += i) st[j] = true;
    }
}

int pw[maxn];

inline int get(int n, int p) {
    int s = 0;
    while (n) s += n/p, n /= p;
    return s;
}

void multi(vector<ll>& res, int b) {
    ll t = 0;
    for (int i = 0; i < res.size(); i++) {
        t += res[i] * b;
        res[i] = t % 100000000, t /= 100000000;
    }
    while (t) res.push_back(t % 100000000), t /= 100000000;
}

void out(const vector<ll>& res) {
    printf("%lld", res.back());
    for (int i = res.size()-2; i >= 0; i--) {
        printf("%08lld", res[i]);
    }
    printf("\n");
}

void init() {
    //
}

int main() {
    freopen("input.txt", "r", stdin);
    cin >> n;

    // get primes
    get_primes();

    // divide factorial
    for (auto p : primes) pw[p] = get(2*n, p) - 2 * get(n, p);

    // divide
    int x = n+1;
    for (auto p : primes) if (p <= x) {
        int s = 0;
        while (x % p == 0) s++, x /= p;
        pw[p] -= s;
    }

    // multi
    vector<ll> ans;
    ans.push_back(1);
    for (auto p : primes) {
        for (int j = 0; j < pw[p]; j++) multi(ans, p);
    }

    // output
    out(ans);
}