【2021.3.2】朴素dijkstra算法 适用于稠密图

csdn：https://blog.csdn.net/qq_36426650/article/details/114282401

要求

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。
输入第一行包含整数n和m。接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。
输出一个整数，表示1号点到n号点的最短距离。如果路径不存在，则输出-1。
结点个数范围 $1\leq n \leq 500$，边个数范围 $1\leq m \leq 10^5$

示例：

给定一个正权边图：

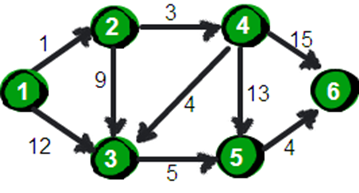
使用邻接矩阵存储：

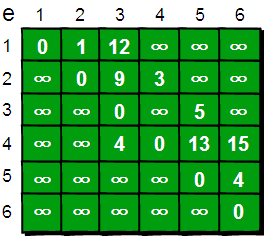
定义一个dist数组，表示存储第i个结点到第1个结点的最短距离，定义一个vis数组表示当前结点是否已经确定
每次从未选择的结点中取出一个最小值，并将对应的结点i的vis[i]值标记为1，表示确定其为最短距离。其次对结点i的所有邻接点，更新这些邻接点的最短距离。

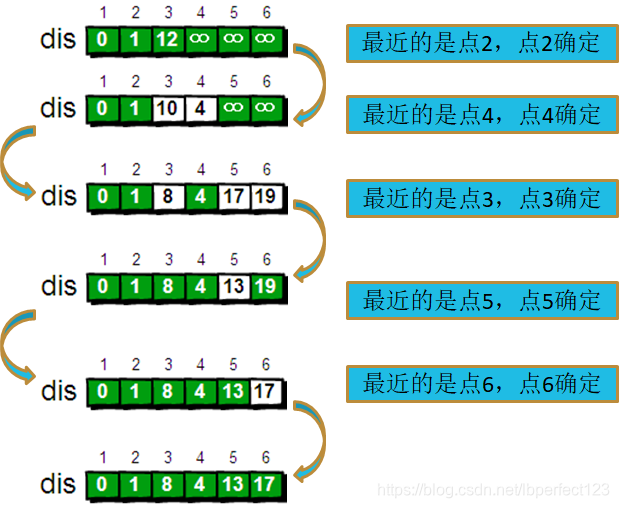
代码模板

// 因为结点的个数是百级，所以是稠密图，可以使用朴素的dijkstra算法，使用邻接矩阵存储图
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int M = 505;
int a[M][M]; // 邻接矩阵
int dist[M]; // 每个点到起始点的距离
int vis[M]; // 判断当前的结点是否已经被选择（被选择的结点说明已经确定了其到1号结点的最短距离）
int n, m;
int x, y, z;
int dijkstra() {
    // 初始化所有的距离为无穷大
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0; // 1号结点的距离自身是0
    for(int i = 0; i < n - 1; i ++) { // 除了1号结点外，每次新增一个结点
        // 从未被选择的结点中，寻找一个距离最短的，其一定是确定的值
        int min_j = -1;
        for(int j = 1; j <= n; j ++) { // 结点编号是从1开始的
            if(!vis[j] && (min_j == -1 || dist[j] < dist[min_j])) { // 寻找到一个最小的距离
                min_j = j;
            }
        }
        vis[min_j] = 1; // 当前最短距离的这个元素一定是确定的，则标记为选择
        // 遍历新加入的这个结点的所有邻接结点，更新距离
        for(int j = 1; j <= n; j ++) {
            dist[j] = min(dist[j], dist[min_j] + a[min_j][j]);
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main() {
    scanf("%d%d", &n, &m);
    memset(a, 0x3f, sizeof a);
    for(int i = 0; i < m; i ++) {
        scanf("%d%d%d", &x, &y, &z);
        a[x][y] = min(a[x][y], z);
    }
    int res = dijkstra();
    printf("%d", res);
    return 0;
}