题目描述

节点间通路。给定有向图，设计一个算法，找出两个节点之间是否存在一条路径。

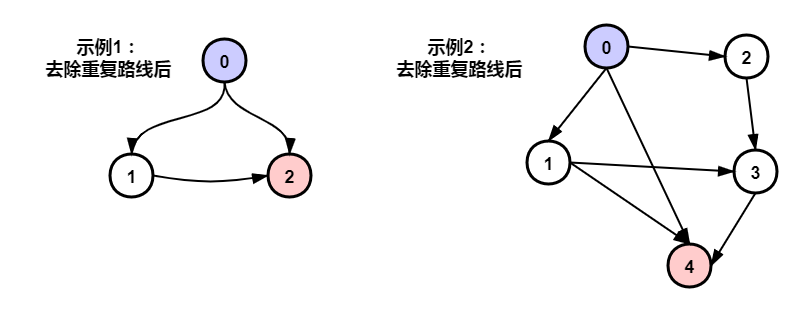
示例1:

 输入：n = 3, graph = [[0, 1], [0, 2], [1, 2], [1, 2]], start = 0, target = 2
 输出：true
示例2:

 输入：n = 5, graph = [[0, 1], [0, 2], [0, 4], [0, 4], [0, 1], [1, 3], 
 [1, 4], [1, 3], [2, 3], [3, 4]], start = 0, target = 4
 输出 true
提示：

节点数量n在[0, 1e5]范围内。
节点编号大于等于 0 小于 n。
图中可能存在自环和平行边。

算法1

(dfs)

使用set数组记录图的结构

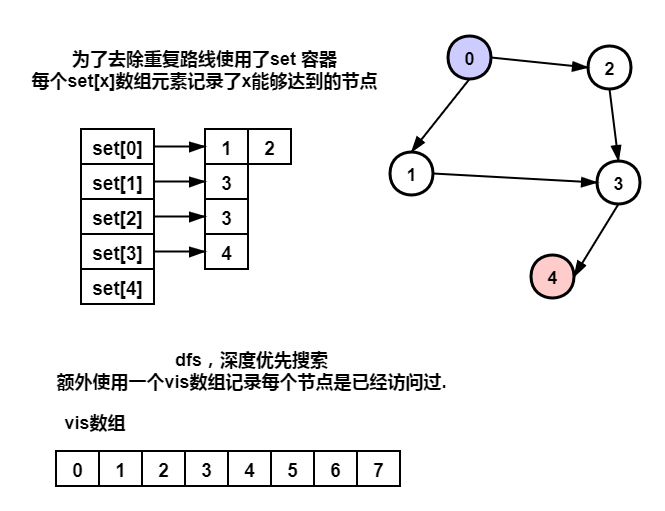
进行DFS

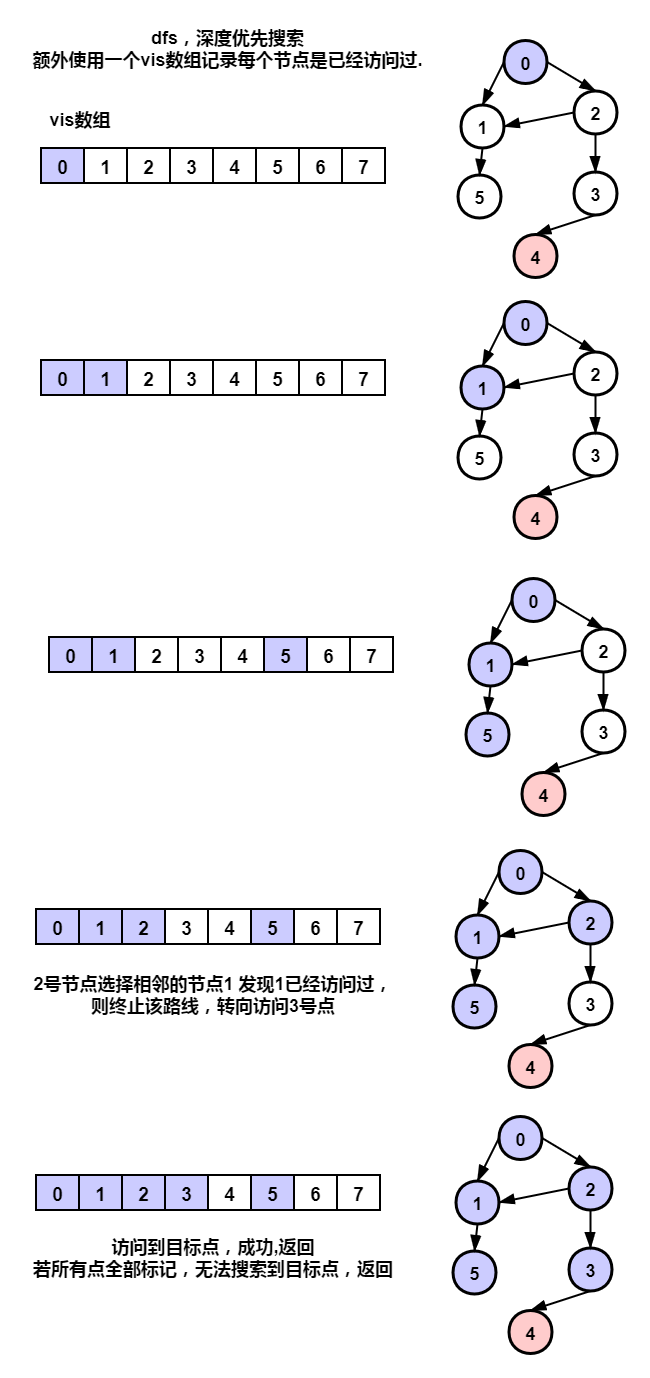
C++ 代码

class Solution {
public:
    set<int> ss[100010];
    int vis[100010];
    bool dfs(int curr,int target)
    {
        bool ret=false;
        if(curr == target) return true;

        //标记当前点已经访问过
        vis[curr] = 1;
        for(auto& e:ss[curr]){
            if(vis[e] != 1){
                ret = dfs(e,target);
                if(ret) return ret;
            }      
        }

        return false;
    }

    bool findWhetherExistsPath(int n, vector<vector<int>>& graph, int start, int target) {
        for(int i =0; i < graph.size();i++){
            int a=graph[i][0]; int b = graph[i][1];
            ss[a].insert(b);
        }
        return dfs(start,target);
    }
};

我的视频题解空间