分析

使用tarjan求出所有连通图，然后遍历所有点，将所有连通图的大小计算出来，如果该连通图内有至少两个点x，那么使用公式$$ans+=C_{x}^{2} $$
计算出所有的连通对的总个数。

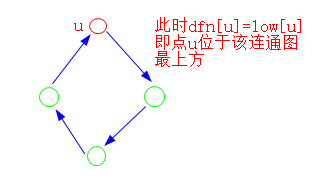
dfn[u]==low[u]时:

C++ 代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e4+10,M = 1e5+10;
int h[N],e[M],ne[M],idx;    //邻接表存储边
int stk[N],top;     //tarjan栈stk，top：栈大小
int dfn[N],low[N],timestamp;    //dfn[u]：遍历到u的时间戳;low[u]：从u开始走能遍历到的最小时间戳;timestamp：时间戳
int id[N],scc_cnt;  //id[i]表示第i个点处于哪个强连通图，scc_cnt：强联通分量个数
bool in_stk[N];     //判断当前点是否在栈stk中。
int n,m;
LL ans;
unordered_map<int,int> mp;  //哈希表用于统计同一个联通图中一共有几个点
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void tarjan(int u)  //tarjan算法求连通图
{
    dfn[u]=low[u]=++timestamp;
    stk[++top]=u,in_stk[u]=true;
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u]=min(low[u],low[j]);
        }
        else if(in_stk[j])
        {
            low[u]=min(low[u],dfn[j]);
        }
    }

    if(dfn[u]==low[u])      //此时说明该点位于一个联通图的最上方 
    {                                                                           
        ++scc_cnt;
        int y;
        do{
            y=stk[top--];
            in_stk[y]=false;
            id[y]=scc_cnt;  //下标为y的点所在的联通图标号为scc_cnt
        }while(y!=u);
    }

}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int a,b;
    for(int i=0;i<m;i++)
    {
        cin>>a>>b;
        add(a,b);
    }
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i])
            tarjan(i);
    }
    for(int i=1;i<=n;i++)   //遍历所有点，统计每个强联通图的大小
    {
        mp[id[i]]++;
    }

    for(auto x:mp)
    {
        if(x.second>1)
        {
            ans+=(LL)(x.second*(x.second-1))/2; //组合公式求和
        }
    }

    cout<<ans;
    return 0;
}