优化效果

定义状态

dp[i][j]表示前i - 1列的方格都已完全覆盖，第i列方格被第i - 1列伸出的方块覆盖后状态为j的所有方案数

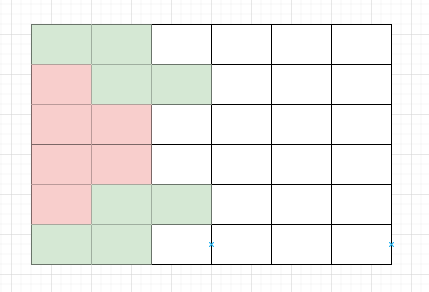
例如，上图表示的就是dp[3][010010]的状态（红色为2 * 1方块，绿色为1 * 2方块）0表示没有覆盖，1表示覆盖

状态转移

我们采用由底至上的递推方式，即由当前状态推出下一列状态的方案数
以某一列的状态而言
1. 如果当前行的格子已被上一列伸出的方块覆盖，则跳过
2. 如果当前行的格子未被覆盖，说明可以放一个1 * 2的方块
3. 如果当前行的格子和下一行的格子都未被覆盖，说明可以放一个2 * 1的方块
4. 此列所有行的格子都覆盖完后，我们便可以得出下一列的合法状态

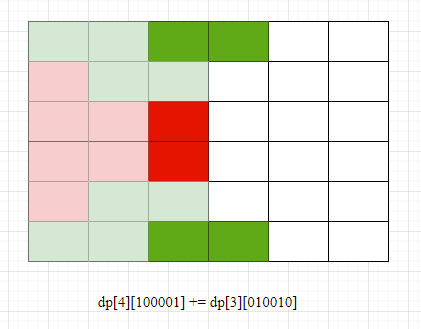
如上图，我们对第3列的状态进行搜索后可到达的其中一种状态

为什么使用搜索？

根据dp数组的定义可知，第一列不可能被上一列伸出的方块覆盖，所以初始化为dp[1][000] = 1，搜索下一列可得：

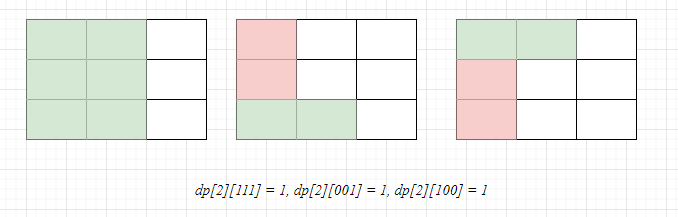
可知第二列可到达的状态只有3种，于是进行第三列的搜索时只需从这3种状态开始dfs，当前阶段总是影响下一阶段，我们只对可到达的进行讨论，并不需要枚举每一种情况
以下是DFS搜索的代码，附详细注释

void dfs(int row, int col, int state, int next) {
    //row为当前行，col为当前列，state为当前列的状态，next为可到达的下一列的状态
    //当前列全覆盖后可到达的下一个状态加上当前状态的方案数
    if (row == n) {
        //当前列所有行都已覆盖完毕
        dp[col + 1][next] += dp[col][state];
        return;
    }
    //如果当前行的格子已被覆盖，跳过
    if (state & (1 << row)) dfs(row + 1, col, state, next);
    else {
        //当前行未被覆盖，可放一个1*2的方块
        dfs(row + 1, col, state, next | (1 << row));
        //当前行和下一行都未被覆盖，可放一个2*1的方块
        if (row + 1 < n && (state & (1 << (row + 1))) == 0) dfs(row + 2, col, state, next);
    }
}

完整C++代码

#include<bits/stdc++.h>
using namespace std;
int n, m;
long long dp[12][2500];
void dfs(int row, int col, int state, int next) {
    //row为当前行，col为当前列，state为当前列的状态，next为可到达的下一列的状态
    //当前列全覆盖后可到达的下一个状态加上当前状态的方案数
    if (row == n) {
        //当前列所有行都已覆盖完毕
        dp[col + 1][next] += dp[col][state];
        return;
    }
    //如果当前行的格子已被覆盖，跳过
    if (state & (1 << row)) dfs(row + 1, col, state, next);
    else {
        //当前行未被覆盖，可放一个1*2的方块
        dfs(row + 1, col, state, next | (1 << row));
        //当前行和下一行都未被覆盖，可放一个2*1的方块
        if (row + 1 < n && (state & (1 << (row + 1))) == 0) dfs(row + 2, col, state, next);
    }
}
int main()
{
    while (scanf("%d%d", &n, &m) && n && m) {
        if (n > m) swap(n, m);
        //因为n行m列和n列m行的方案数等价，所以我们不妨将min(n, m)作为二进制枚举的指数，减少方案数
        memset(dp, 0, sizeof(dp));
        dp[0][0] = 1;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < (1 << n); j++) {
                if (dp[i][j] > 0) {     //筛选出之前搜索过可到达的状态
                    dfs(0, i, j, 0);
                }
            }
        }
        //因为下标从0开始，所以dp[m][0]表示第m + 1列没有任何第m列的方块伸出的方案数
        cout << dp[m][0] << endl;
    }
    return 0;
}