题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

样例

输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

算法1

差分矩阵

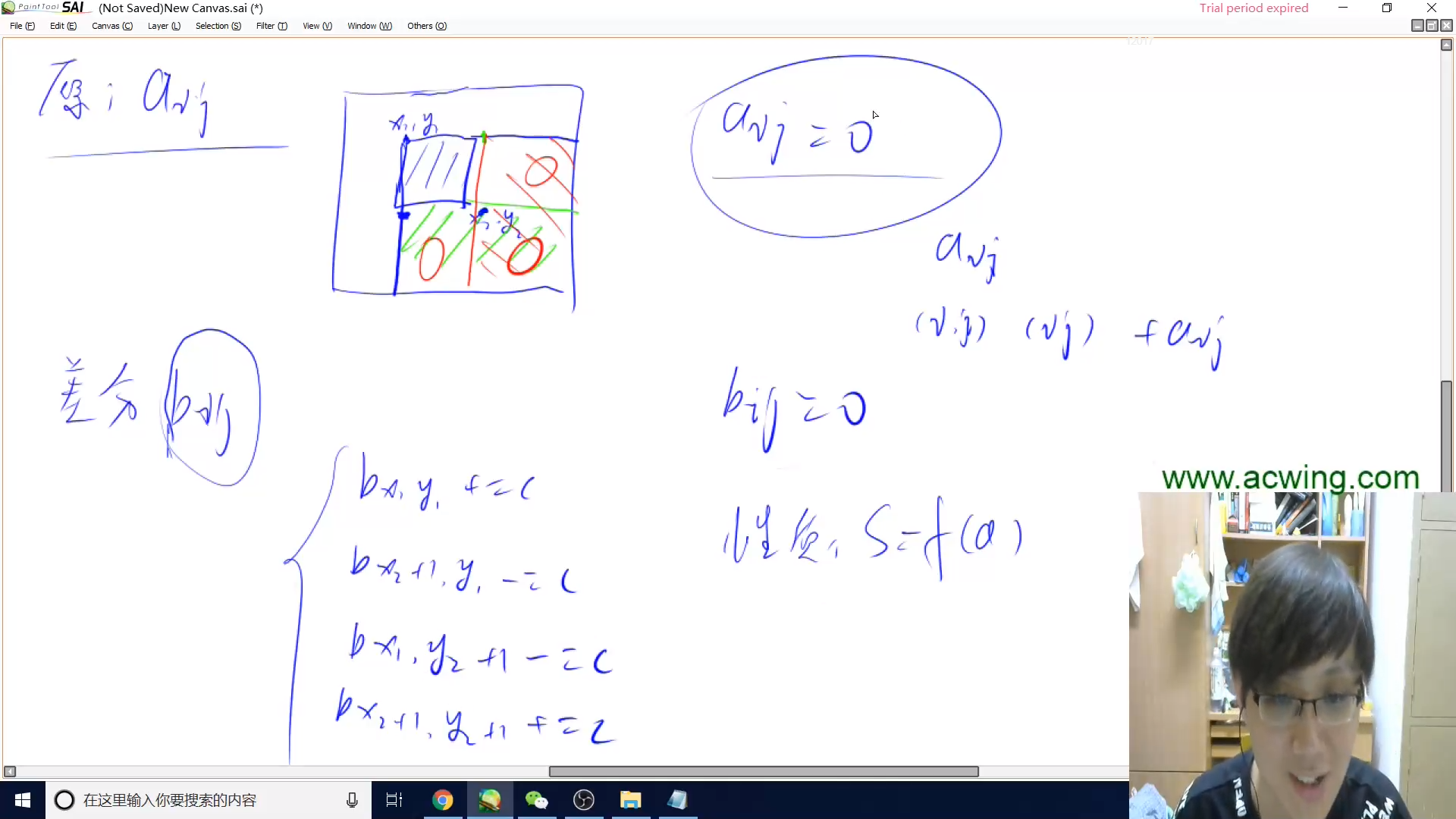
时间复杂度

python 代码

#二维差分
#给其中一个子矩阵加上一个值
#
def insert(x1,y1,x2,y2,c):
    b[x1][y1]+=c
    b[x2+1][y1]-=c
    b[x1][y2+1]-=c
    b[x2+1][y2+1]+=c


if __name__ == "__main__":
    n,m,q = map(int,input().split())
    a = [[0]*(m+2)]
    b = [[0]*(m+2) for _ in range(n+2)]
    for i in range(n):
        a.append([0]+list(map(int,input().split())))
    for i in range(1,n+1):
        for j in range(1,m+1):
            insert(i,j,i,j,a[i][j])
    for i in range(q):
        x1,y1,x2,y2,c = map(int,input().split())
        insert(x1,y1,x2,y2,c)
    for i in range(1,n+1):
        for j in range(1,m+1):
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1]
    for i in range(1,n+1):
        for j in range(1,m+1):
            print(b[i][j],end =" ")
        print()