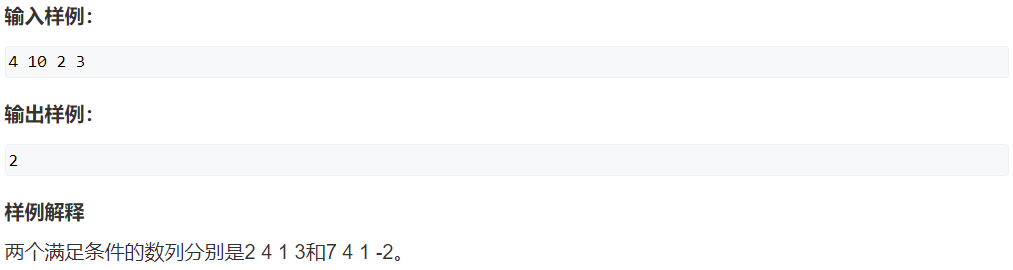
题目描述

算法

(动态规划：类似背包问题的组合问题)

假设第一项是x(未定), 之后每步进行的操作为+Di, 其中Di有两种取值: Di = {+a, -b}.
那么, 这n项的和可以写成：$$S = x + (x + D_1) + (x + D_1 + D_2) + … + (x + D_1 + D_2 + … + D_{n-1})$$
整理得: $$S = nx + (n - 1)D_1 + (n - 2)D_2 + … + 2D_{n - 2} + D_{n-1}$$
发现，要求符合规则的数列个数，只要满足上式，数列就符合题述规则。继续整理：$$x=[S-[(n-1)D_1+(n-2)D_2+…+2D_{n-2}+D_{n-1}]]/n$$.
令$$C=(n-1)D_1+(n-2)D_2+…+2D_{n-2}+D_{n-1}$$
只要满足，S模n的值与C模n的值相同, 就能得到一个合适的x值，也就代表了正确的序列规则。

设dp[i][j]表示, 前i项(这里不包括第一项x)的和模上n余j的方案数量. 下面考虑状态转移方程：
对于$$C=(n-1)D_1+(n-2)D_2+…+2D_{n-2}+D_{n-1}$$,在这里交换一下 $D_i$ 和 $D_{n-i}$ 的表示含义(因为$D_i$本就是一个不定量，有两种取值，这里仅交换含义，表示的等式意义是一样的，而不是直接交换已经确定的 $D_i$ 和 $D_{n-i}$ 对应的实际值). 那么C就可等价于$$C=D_1+2D_2+…+(n-2)D_{n-2}+(n-1)D_{n-1}$$

时间复杂度

$O(n^2)$

参考文献

C++ 代码

blablabla

算法2

(暴力枚举) $O(n^2)$

blablabla

时间复杂度

参考文献

C++ 代码

blablabla