题目描述

假定有一个无限长的数轴，数轴上每个坐标上的数都是0。

现在，我们首先进行 n 次操作，每次操作将某一位置x上的数加c。

接下来，进行 m 次询问，每个询问包含两个整数l和r，你需要求出在区间[l, r]之间的所有数的和。

输入格式
第一行包含两个整数n和m。

接下来 n 行，每行包含两个整数x和c。

再接下里 m 行，每行包含两个整数l和r。

输出格式
共m行，每行输出一个询问中所求的区间内数字和。

数据范围
−10^9≤x≤10^9,
1≤n,m≤10^5,
−10^9≤l≤r≤10^9,
−10000≤c≤10000

样例

输入样例：
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例：
8
0
5

算法1

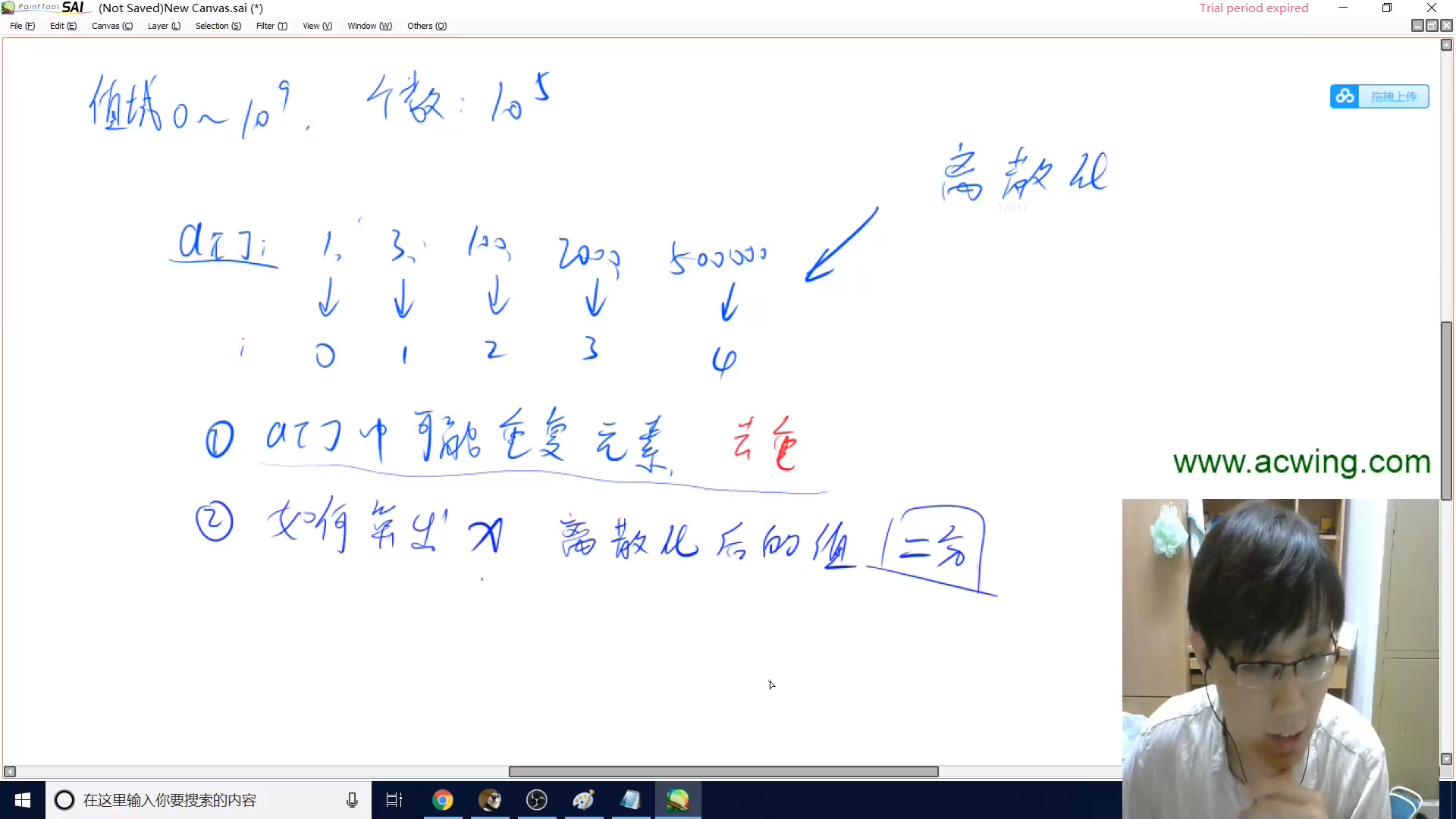
离散化

区间较大，且很稀疏，因此要进行空间优化。
1.把所有用到的下标存到alls里面
2.alls中可能有重复的元素，要去重
3.把alls的值（原数组用到的下标）映射为新的下标
4.如原数组用到的下标为[1,3,4,6,7,8],映射为1,2,3,4,5,6,用数组a保存
这里用二分法求出x离散化后的值,实际上返回的就是x在alls中的下标+1。

python 代码

def find(x):        #找的是当前值在所有用到的值在alls中的下标+1
    l=0
    r = len(alls)-1
    while l<r:
        mid = (l+r)//2
        if(alls[mid]>=x):
            r=mid
        else:
            l=mid+1
    return r+1                  #这里+1是因为后面方便计算a数组的前缀和
    # return alls.index(x)+1    #这么写可以通过8/10个数据，通过不了是因为超时。所以用二分找下标效率高一点。


if __name__ == "__main__":
    N = 300010
    n,m = map(int,input().split())
    alls = []       #存所有用到的下标
    add = []        #插入操作
    query = []      #询问操作
    a=[0]*N
    s=[0]*N

    for i in range(n):
        x,c = map(int,input().split())
        add.append((x,c))
        alls.append(x)
    for i in range(m):
        l,r = map(int,input().split())
        query.append((l,r))
        alls.append(l)
        alls.append(r)
    #排序去重
    alls = list(set(sorted(alls)))
    #处理插入
    for i in range(len(add)):
        x = find(add[i][0])
        a[x]+=add[i][1]
    #预处理前缀和
    for i in range(1,len(alls)+1):
        s[i] = s[i-1]+a[i]

    #处理询问
    for i in range(len(query)):
        l = find(query[i][0])
        r = find(query[i][1])
        print(s[r]-s[l-1])