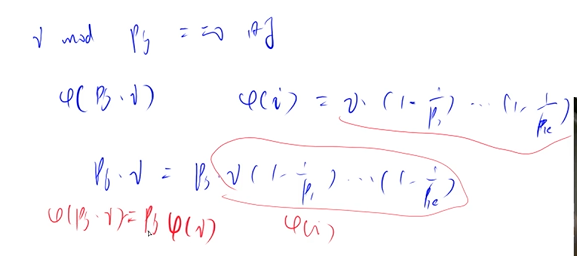
pj是i的质因子，所以pj * i的质因子和i的质因子都相同，因此推出二者欧拉函数关系

pj不是i的质因子，所以pj * i的质因子比i的质因子多一个pj

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;

int primes[N],cnt;
int phi[N];
bool st[N];


int get_eulers(int n){
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!st[i]){
            primes[cnt++]=i;
            phi[i]=i-1;
        }
        for(int j=0;primes[j]<=n/i;j++){
            st[primes[j]*i]=true;
            if(i%primes[j]==0){
                phi[primes[j]*i]=phi[i]*primes[j];
                break;
            }
            phi[primes[j]*i]=phi[i]*(primes[j]-1);
        }
    }
}

int main(){
    int n;
    cin>>n;

    get_eulers(n);

    ll res=0;
    for(int i=1;i<=n;i++){
        res+=phi[i];
    }
    cout<<res<<endl;
}